题目内容
【题目】已知曲线![]()
(1)若![]() ,过点
,过点![]() 的直线
的直线![]() 交曲线
交曲线![]() 于
于![]() 两点,且
两点,且![]() ,求直线
,求直线![]() 的方程;
的方程;
(2)若曲线![]() 表示圆时,已知圆
表示圆时,已知圆![]() 与圆
与圆![]() 交于
交于![]() 两点,若弦
两点,若弦![]() 所在的直线方程为
所在的直线方程为![]() ,
, ![]() 为圆
为圆![]() 的直径,且圆
的直径,且圆![]() 过原点,求实数
过原点,求实数![]() 的值.
的值.
【答案】(1)![]() 或
或![]() (即
(即![]() ) ;(2)
) ;(2) ![]() .
.
【解析】试题分析:(1)由已知条件推导出圆心C(1,2),2为半径,由此利用点到直线的距离公式结合已知条件能求出m=1.
(2)求出圆![]() 的方程,两圆相减得公共弦方程
的方程,两圆相减得公共弦方程![]() ,即得m.
,即得m.
试题解析:
(1) 当![]() 时, 曲线C是以
时, 曲线C是以![]() 为圆心,2为半径的圆,
为圆心,2为半径的圆,
若直线![]() 的斜率不存在,显然不符,
的斜率不存在,显然不符,
故可直线![]() 为:
为: ![]() ,即
,即![]() .
.
由题意知,圆心![]() 到直线
到直线![]() 的距离等于
的距离等于![]() ,
,
即: ![]()
解得![]() 或
或![]() .故的方程
.故的方程![]() 或
或![]() (即
(即![]() )
)
(2)由曲线C表示圆![]() ,即
,即![]() ,
,
所以圆心C(1,2),半径![]() ,则必有
,则必有![]() .
.
设过圆心![]() 且与
且与![]() 垂直的直线为:
垂直的直线为: ![]() ,解得
,解得![]() ;
;
![]() ,所以,圆心
,所以,圆心![]()
又因为圆![]() 过原点,则
过原点,则![]() ;
;
所以圆![]() 的方程为
的方程为![]() ,整理得:
,整理得: ![]() ;
;
因为![]() 为两圆的公共弦,两圆方程相减得:
为两圆的公共弦,两圆方程相减得: ![]() ;
;
所以![]() 为直线
为直线![]() 的方程;又因为
的方程;又因为![]() ;所以
;所以![]() .
.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
【题目】假设关于某种设备的使用年限![]() (年)与所支出的维修费用
(年)与所支出的维修费用![]() (万元)有如下统计资料:
(万元)有如下统计资料:
x | 2 | 3 | 4 | 5 | 6 |
y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
已知![]() ,
, ![]() .
.
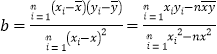 ,
, ![]()
(1)求![]() ,
, ![]() ;
;
(2)若 ![]() 与
与![]() 具有线性相关关系,求出线性回归方程;
具有线性相关关系,求出线性回归方程;
(3)估计使用年限为10年时,维修费用约是多少?