题目内容
某车间甲组有10名工人,其中有4名女工人;乙组有10名工人,其中有6名女工人。分别从甲、乙两组中各抽取2名工人进行技术考核。每此抽取互不影响。
(1)求从甲组抽取的工人中恰有1名女工人的概率;
(2)求抽取的4名工人中恰有2名男工人的概率..
(1)求从甲组抽取的工人中恰有1名女工人的概率;
(2)求抽取的4名工人中恰有2名男工人的概率..
(I)由于甲、乙两组各有10名工人,根据分层抽样原理,要从甲、乙两组中共抽取4名工人进行技术考核,则从每组各抽取2名工人。
(II)记A表示事件:从甲组抽取的工人中恰有1名女工人,则
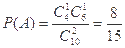
(III)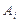 表示事件:从甲组抽取的2名工人中恰有
表示事件:从甲组抽取的2名工人中恰有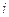 名男工人,
名男工人,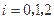
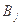 表示事件:从乙组抽取的2名工人中恰有
表示事件:从乙组抽取的2名工人中恰有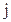 名男工人,
名男工人,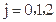
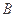 表示事件:抽取的4名工人中恰有2名男工人。.
表示事件:抽取的4名工人中恰有2名男工人。.
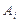 与
与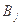 独立,
独立,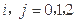 ,且
,且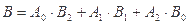
故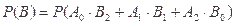
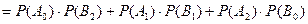
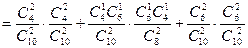
(II)记A表示事件:从甲组抽取的工人中恰有1名女工人,则
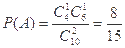
(III)
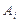 表示事件:从甲组抽取的2名工人中恰有
表示事件:从甲组抽取的2名工人中恰有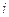 名男工人,
名男工人,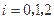
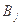 表示事件:从乙组抽取的2名工人中恰有
表示事件:从乙组抽取的2名工人中恰有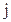 名男工人,
名男工人,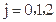
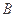 表示事件:抽取的4名工人中恰有2名男工人。.
表示事件:抽取的4名工人中恰有2名男工人。. 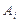 与
与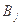 独立,
独立,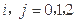 ,且
,且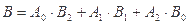
故
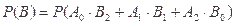
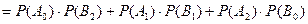
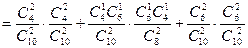
本题考查概率统计知识,要求有正确理解分层抽样的方法及利用分类原理处理事件概率的能力,第一问直接利用分层统计原理即可得人数,第二问注意要用组合公式得出概率,第三问关键是理解清楚题意以及恰有2名男工人的具体含义,从而正确分类求概率。

练习册系列答案
相关题目
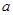 ,
,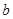 分别为先后掷一枚骰子得到的点数,则在先后两次出现的点数有5的条
分别为先后掷一枚骰子得到的点数,则在先后两次出现的点数有5的条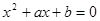 有实根的概率为 ( )
有实根的概率为 ( ) 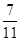
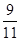
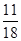
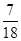
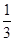
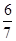
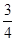
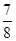
 :
: ,如果
,如果 是数列
是数列 项和,那么
项和,那么 的概率是( )
的概率是( ) 、
、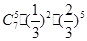
 、
、
 、
、
 、
、
 b,则直线
b,则直线 与圆
与圆 相交的概率为 .
相交的概率为 .