题目内容
在△ABC中,角A,B,C的对边分别为a,b,c,若acos2 +ccos2
+ccos2 =
= b.
b.
(1)求证:a,b,c成等差数列;
(2)若∠B=60°,b=4,求△ABC的面积.
(1)见解析(2)4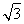
【解析】(1)acos2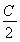 +ccos2
+ccos2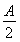 =a·
=a·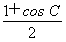 +c·
+c·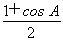 =
= b,
b,
即a(1+cos C)+c(1+cos A)=3b.由正弦定理得:
sin A+sin Acos C+sin C+cos Asin C=3sin B,
即sin A+sin C+sin(A+C)=3sin B,∴sin A+sin C=2sin B.
由正弦定理得,a+c=2b,故a,b,c成等差数列.
(2)由∠B=60°,b=4及余弦定理得:42=a2+c2-2accos 60°,
∴(a+c)2-3ac=16,
又由(1)知a+c=2b,代入上式得4b2-3ac=16,解得ac=16,
∴△ABC的面积S=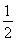 acsin B=
acsin B=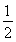 acsin 60°=4
acsin 60°=4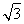 .
.

练习册系列答案
相关题目


















