题目内容
已知a,b,c分别是三角形ABC的角A、B、C所对边,且a,b,c成等差数列,公差d≠0;
(1)求证:
,
,
不可能成等差数列.
(2)求证:0°<B<60°.
(1)求证:
| 1 |
| a |
| 1 |
| b |
| 1 |
| c |
(2)求证:0°<B<60°.
(1)证明:假设
,
,
成等差数列,则有
-
=
-
,从而
=
,
因为a,b,c成等差数列,d≠0;所以a-b=b-c=-d,
故
=
,从而ab=bc即a=c,这与已知d≠0相矛盾.
所以
,
,
不可能成等差数列.
(2)∵
=
.
又因为B为三角形内角,所以,0°<B<60°.
| 1 |
| a |
| 1 |
| b |
| 1 |
| c |
| 1 |
| b |
| 1 |
| a |
| 1 |
| c |
| 1 |
| b |
| a-b |
| ab |
| b-c |
| bc |
因为a,b,c成等差数列,d≠0;所以a-b=b-c=-d,
故
| -d |
| ab |
| -d |
| bc |
所以
| 1 |
| a |
| 1 |
| b |
| 1 |
| c |
(2)∵
|
=
|
又因为B为三角形内角,所以,0°<B<60°.

练习册系列答案
相关题目
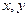 都是正实数,求证:
都是正实数,求证: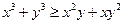 ;
;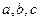 都是正实数,求证:
都是正实数,求证: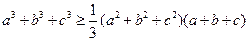 .
.  ≥
≥ .
.
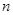 个图包含______个互不重叠的单位正方形。
个图包含______个互不重叠的单位正方形。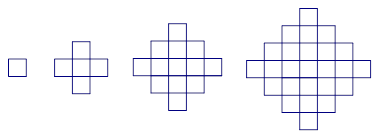
 +
+ +…+
+…+ >
> 的过程中,由n=k推导n=k+1时,不等式的左边增加的式子是________.
的过程中,由n=k推导n=k+1时,不等式的左边增加的式子是________.