题目内容
(1)当n∈N+时,求证:
≤
+
+…+
<1;
(2)当n∈N+时,求证:1+
+
+…+
<2.
| 1 |
| 2 |
| 1 |
| n+1 |
| 1 |
| n+2 |
| 1 |
| 2n |
(2)当n∈N+时,求证:1+
| 1 |
| 22 |
| 1 |
| 32 |
| 1 |
| n2 |
(1)证明:∵
+
+
+…+
≤
+
+…+
<
+
+…+
,
∴
≤
+
+…+
<1,故不等式成立.
(2)证明:∵1+
+
+…+
<1+
+
+
+…+
=1+1-
+
-
+
-
+…+
-
=2-
<2,
即 1+
+
+…+
<2.
| 1 |
| 2n |
| 1 |
| 2n |
| 1 |
| 2n |
| 1 |
| 2n |
| 1 |
| n+1 |
| 1 |
| n+2 |
| 1 |
| 2n |
| 1 |
| n |
| 1 |
| n |
| 1 |
| n |
∴
| 1 |
| 2 |
| 1 |
| n+1 |
| 1 |
| n+2 |
| 1 |
| 2n |
(2)证明:∵1+
| 1 |
| 22 |
| 1 |
| 32 |
| 1 |
| n2 |
| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 1 |
| 3×4 |
| 1 |
| (n-1)×n |
=1+1-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| n-1 |
| 1 |
| n |
| 1 |
| n |
即 1+
| 1 |
| 22 |
| 1 |
| 32 |
| 1 |
| n2 |

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
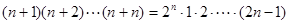 ”(
”( )时,从 “
)时,从 “ ”时,左边应增添的式子是( )
”时,左边应增添的式子是( )



 cosx,满足
cosx,满足 对
对 x∈R都成立,推断
x∈R都成立,推断 为奇函数。
为奇函数。 的面积
的面积 推断:椭圆
推断:椭圆 (a>b>0)的面积s=πab
(a>b>0)的面积s=πab