题目内容
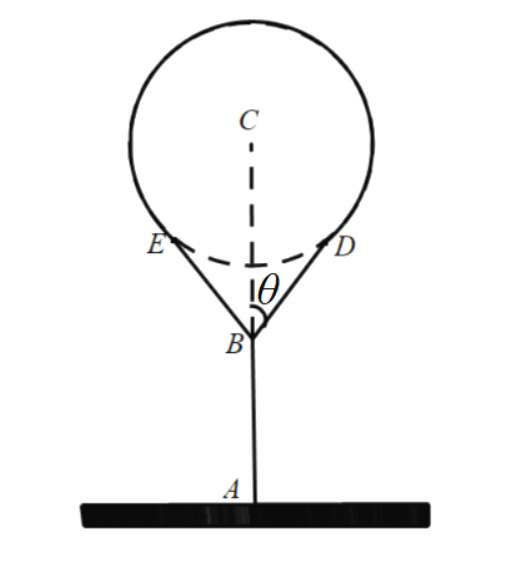
【题目】如图，湖中有一个半径为
千米的圆形小岛，岸边点
与小岛圆心
相距
千米，为方便游人到小岛观光，从点向小岛建三段栈道
，
，
，湖面上的点
在线段
上，且，均与圆相切，切点分别为
，
，其中栈道，，和小岛在同一个平面上.沿圆的优弧（圆上实线部分）上再修建栈道
.记
为
.
用表示栈道的总长度
，并确定
的取值范围；
求当为何值时，栈道总长度最短.
【答案】
，
；
当
时，栈道总长度最短.
【解析】
连
，
，由切线长定理知：
，
，
，
，即
，
，
则，
，进而确定
的取值范围；
根据
求导得
，利用增减性算出
，进而求
得取值.
解：连，，由切线长定理知：，，
，又
，
，故
，
则劣弧
的长为
，因此，优弧的长为
，
又
，故，，即，，
所以，，，则；
，，其中，，
|
|
|
|
| - | 0 | + |
| 单调递减 | 极小值 | 单调递增 |
故时，
所以当时，栈道总长度最短.
练习册系列答案
名校课堂系列答案
相关题目
