题目内容
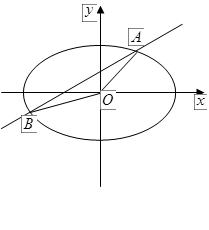
(本题14分)如图,直线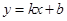 与椭圆
与椭圆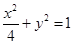 交于
交于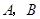 两点,记
两点,记 的面积为
的面积为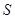 .
.
(I)求在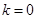 ,
,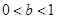 的条件下,
的条件下,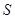 的最大值;
的最大值;
(II)当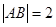 ,
,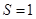 时,求直线
时,求直线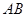 的方程.
的方程.
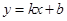 与椭圆
与椭圆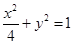 交于
交于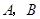 两点,记
两点,记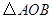 的面积为
的面积为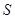 .
.
(I)求在
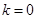 ,
,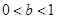 的条件下,
的条件下,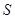 的最大值;
的最大值;(II)当
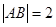 ,
,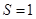 时,求直线
时,求直线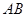 的方程.
的方程.(I)当且仅当 时,
时,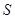 取到最大值
取到最大值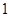 .
.
(II)直线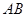 的方程是
的方程是
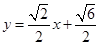 或
或 或
或 ,或
,或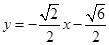 。
。
 时,
时,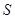 取到最大值
取到最大值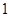 .
.(II)直线
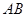 的方程是
的方程是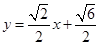 或
或 或
或 ,或
,或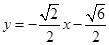 。
。(Ⅰ)解:设点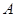 的坐标为
的坐标为 ,点
,点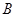 的坐标为
的坐标为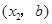 ,
,
由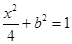 ,解得
,解得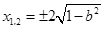 ,
,
所以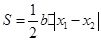
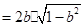
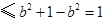 .
.
当且仅当 时,
时,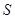 取到最大值
取到最大值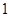 .
.
(Ⅱ)解:由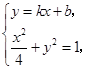
得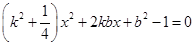 ,
,
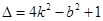 ,
,
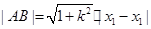
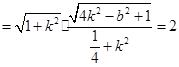 . ②
. ②
设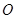 到
到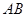 的距离为
的距离为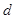 ,则
,则
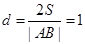 ,
,
又因为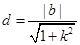 ,
,
所以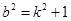 ,代入②式并整理,得
,代入②式并整理,得
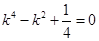 ,
,
解得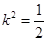 ,
,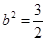 ,代入①式检验,
,代入①式检验,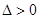 ,
,
故直线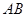 的方程是
的方程是
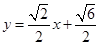 或
或 或
或 ,或
,或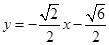 .
.
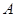 的坐标为
的坐标为 ,点
,点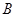 的坐标为
的坐标为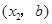 ,
,由
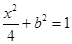 ,解得
,解得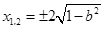 ,
,所以
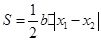
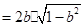
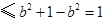 .
.当且仅当
 时,
时,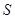 取到最大值
取到最大值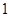 .
.(Ⅱ)解:由
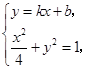
得
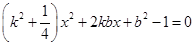 ,
,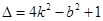 ,
,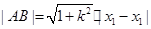
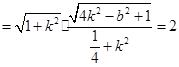 . ②
. ②设
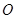 到
到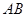 的距离为
的距离为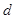 ,则
,则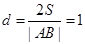 ,
,又因为
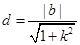 ,
,所以
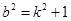 ,代入②式并整理,得
,代入②式并整理,得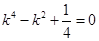 ,
,解得
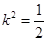 ,
,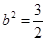 ,代入①式检验,
,代入①式检验,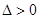 ,
,故直线
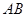 的方程是
的方程是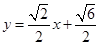 或
或 或
或 ,或
,或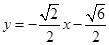 .
.
练习册系列答案
相关题目
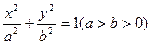 的离心率是
的离心率是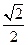 ,右焦点
,右焦点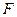 到上顶点的距离为
到上顶点的距离为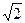 ,点
,点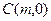 是线段
是线段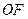 上的一个动点.
上的一个动点.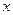 轴不垂直的直线
轴不垂直的直线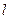 与椭圆交于
与椭圆交于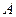 、
、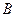 两点,使得
两点,使得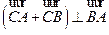 ,并说明理由.
,并说明理由.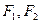 分别为椭圆
分别为椭圆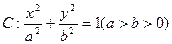 的左、右两个焦点.
的左、右两个焦点.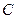 上的点
上的点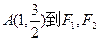 两点的距离之和等于4,
两点的距离之和等于4,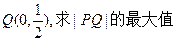 。
。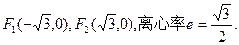
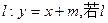 与此椭圆相交于不同的两点,求m的取值范围.
与此椭圆相交于不同的两点,求m的取值范围.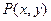 是椭圆
是椭圆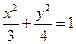 上的动点。
上的动点。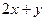 的取值范围
的取值范围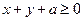 恒成立,求实数a的取值范围。
恒成立,求实数a的取值范围。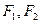 是椭圆
是椭圆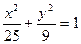 的两个焦点,过
的两个焦点,过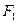 作直线与椭圆交于A,B两点,
作直线与椭圆交于A,B两点,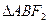 的周长为
的周长为 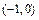 、B
、B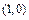 ,以AB为一腰作使∠DAB=
,以AB为一腰作使∠DAB=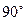 直角梯形ABCD,且
直角梯形ABCD,且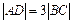 ,CD中点的纵坐标为1.若椭圆以A、B为焦点且经过点D,则此椭圆的方程为
,CD中点的纵坐标为1.若椭圆以A、B为焦点且经过点D,则此椭圆的方程为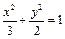 B.
B.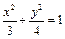 C.
C.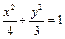 D.
D.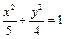
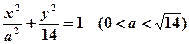 的两焦点为
的两焦点为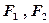 ,现将坐标平面沿
,现将坐标平面沿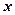 轴折成二面角,二面角的度数为
轴折成二面角,二面角的度数为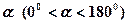 ,已知折起后两焦点的距离
,已知折起后两焦点的距离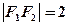 ,则满足题设的一组数值:
,则满足题设的一组数值:
 (只需写出一组就可以,不必写出所有情况)
(只需写出一组就可以,不必写出所有情况)