题目内容
5.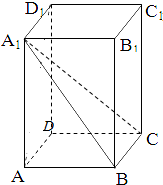 如图,在长方体ABCD-A1B1C1D1中,DA=DC=1,DD1=2,点P在棱CC1上.
如图,在长方体ABCD-A1B1C1D1中,DA=DC=1,DD1=2,点P在棱CC1上.(1)求异面直线AB与A1C所成角的余弦值;
(2)若∠A1PB=90°,记二面角A-A1B-P的平面角为θ,求sinθ
分析 (1)容易找到∠DCA1便是异面直线AB与A1C所成角,而△A1CD为直角三角形,从而根据已知的边长可求出cos∠DCA1;
(2)首先以D为原点,直线DA,DC,DD1为x,y,z轴建立空间直角坐标系,容易判断$\overrightarrow{DA}$为平面AA1B的法向量,而根据P点在棱CC1上且A1P⊥BP即可求出点P的坐标.设平面PA1B的法向量为$\overrightarrow{n}=({x}_{1},{y}_{1},{z}_{1})$,而根据$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{P{A}_{1}}=0}\\{\overrightarrow{n}•\overrightarrow{PB}=0}\end{array}\right.$即可求出$\overrightarrow{n}$,从而根据$cosθ=-cos<\overrightarrow{n},\overrightarrow{DA}>$求出cosθ,从而求出sinθ.
解答  解:(1)如图,连接A1D;
解:(1)如图,连接A1D;
∵DC∥AB,∴∠A1CD便是异面直线AB与A1C所成的角;
在Rt△A1CD中,∠A1DC=90°,${A}_{1}D=\sqrt{5},DC=1$,${A}_{1}C=\sqrt{6}$;
∴$cos∠{A}_{1}CD=\frac{\sqrt{6}}{6}$;
即异面直线AB与A1C所成角的余弦值为$\frac{\sqrt{6}}{6}$;
(2)以D为原点,边DA,DC,DD1所在直线为x,y,z轴建立空间直角坐标系,则:
D(0,0,0),A(1,0,0),B(1,1,0),A1(1,0,2);
显然$\overrightarrow{DA}=(1,0,0)$为平面AA1B的法向量;
∵P在棱CC1上,∴设P(0,1,z),0≤z≤2;
∴$\overrightarrow{P{A}_{1}}=(1,-1,2-z)$,$\overrightarrow{PB}=(1,0,-z)$;
∵∠A1PB=90°;
∴$\overrightarrow{P{A}_{1}}•\overrightarrow{PB}=0$;
∴1-z(2-z)=0;
解得z=1;
∴P(0,1,1);
设平面PA1B的法向量为$\overrightarrow{n}=({x}_{1},{y}_{1},{z}_{1})$,则:$\overrightarrow{n}⊥\overrightarrow{P{A}_{1}},\overrightarrow{n}⊥\overrightarrow{PB}$;
∴$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{P{A}_{1}}=0}\\{\overrightarrow{n}•\overrightarrow{PB}=0}\end{array}\right.$;
∴$\left\{\begin{array}{l}{{x}_{1}-{y}_{1}+{z}_{1}=0}\\{{x}_{1}-{z}_{1}=0}\end{array}\right.$;
∴$\left\{\begin{array}{l}{{x}_{1}={z}_{1}}\\{{y}_{1}=2{z}_{1}}\end{array}\right.$,取z1=1,∴$\overrightarrow{n}=(1,2,1)$;
∴$cosθ=-cos<\overrightarrow{DA},\overrightarrow{n}>$=$-\frac{1}{\sqrt{6}}$;
∴sinθ=$\sqrt{1-\frac{1}{6}}=\frac{\sqrt{30}}{6}$.
点评 考查异面直线所成角的概念及求法,直角三角形边角的关系,建立空间直角坐标系,利用空间向量解决二面角问题的方法,平面法向量的概念及求法,两非零向量垂直的充要条件,以及向量夹角余弦的坐标公式.

| A. | 1 | B. | 2 | C. | $\sqrt{5}$ | D. | $2\sqrt{5}$ |
 如图,A、B是圆O上的两点,∠AOB=120°,C是AB弧的中点.
如图,A、B是圆O上的两点,∠AOB=120°,C是AB弧的中点. 如图,|$\overrightarrow{OA}$|=|$\overrightarrow{OB}$|=1,$\overrightarrow{OA}$、$\overrightarrow{OB}$的夹角是120°,$\overrightarrow{OA}$、$\overrightarrow{OC}$的夹角为30°,$\overrightarrow{OC}$=5,$\overrightarrow{OA}$、$\overrightarrow{OB}$表示$\overrightarrow{OC}$.
如图,|$\overrightarrow{OA}$|=|$\overrightarrow{OB}$|=1,$\overrightarrow{OA}$、$\overrightarrow{OB}$的夹角是120°,$\overrightarrow{OA}$、$\overrightarrow{OC}$的夹角为30°,$\overrightarrow{OC}$=5,$\overrightarrow{OA}$、$\overrightarrow{OB}$表示$\overrightarrow{OC}$. 如图,四棱锥P-ABCD中,PA⊥底面ABCD,∠ABC=∠ADC=90°,CB=CD=1,∠BCD=120°,E为线段BP的靠近点B的一个四等分点,AE⊥PC.
如图,四棱锥P-ABCD中,PA⊥底面ABCD,∠ABC=∠ADC=90°,CB=CD=1,∠BCD=120°,E为线段BP的靠近点B的一个四等分点,AE⊥PC.