题目内容
15. 如图,|$\overrightarrow{OA}$|=|$\overrightarrow{OB}$|=1,$\overrightarrow{OA}$、$\overrightarrow{OB}$的夹角是120°,$\overrightarrow{OA}$、$\overrightarrow{OC}$的夹角为30°,$\overrightarrow{OC}$=5,$\overrightarrow{OA}$、$\overrightarrow{OB}$表示$\overrightarrow{OC}$.
如图,|$\overrightarrow{OA}$|=|$\overrightarrow{OB}$|=1,$\overrightarrow{OA}$、$\overrightarrow{OB}$的夹角是120°,$\overrightarrow{OA}$、$\overrightarrow{OC}$的夹角为30°,$\overrightarrow{OC}$=5,$\overrightarrow{OA}$、$\overrightarrow{OB}$表示$\overrightarrow{OC}$.
分析 如图所示,建立直角坐标系,设$\overrightarrow{OC}$=m$\overrightarrow{OA}$+n$\overrightarrow{OB}$,利用向量坐标运算、向量基本定理即可得出m、n的值.
解答 解:如图所示,建立直角坐标系.,则由题意可得C($\frac{5}{2}$$\sqrt{3}$,$\frac{5}{2}$)、A(1,0)、B(-$\frac{1}{2}$,$\frac{\sqrt{3}}{2}$).
设$\overrightarrow{OC}$=m$\overrightarrow{OA}$+n$\overrightarrow{OB}$,则($\frac{5}{2}$$\sqrt{3}$,$\frac{5}{2}$)=m(1,0)+n(-$\frac{1}{2}$,$\frac{\sqrt{3}}{2}$)=(m-$\frac{1}{2}$n,$\frac{\sqrt{3}}{2}$n).
∴m-$\frac{1}{2}$n=$\frac{5\sqrt{3}}{2}$,$\frac{\sqrt{3}}{2}$n=$\frac{5}{2}$.
求得m=$\frac{10\sqrt{3}}{3}$,n=$\frac{5\sqrt{3}}{3}$,∴$\overrightarrow{OC}$=$\frac{10\sqrt{3}}{3}$$\overrightarrow{OA}$+$\frac{5\sqrt{3}}{3}$$\overrightarrow{OB}$.
点评 本题考查了向量坐标运算、向量基本定理,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案
相关题目
3.直线y=-2x+2恰好经过椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1的右焦点和上顶点,则椭圆的离心率等于( )
| A. | $\frac{\sqrt{5}}{5}$ | B. | $\frac{1}{2}$ | C. | $\frac{2\sqrt{5}}{5}$ | D. | $\frac{\sqrt{5}}{2}$ |
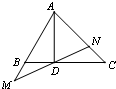 如图,在△ABC中,$\overrightarrow{AD}$•$\overrightarrow{BC}$=0,$\overrightarrow{BC}$=3$\overrightarrow{BD}$,过点D的直线分别交直线AB,AC于点M,N.若$\overrightarrow{AM}$=λ$\overrightarrow{AB}$,$\overrightarrow{AN}$=μ$\overrightarrow{AC}$(λ>0,μ>0),则λ+2μ的最小值是$\frac{8}{3}$.
如图,在△ABC中,$\overrightarrow{AD}$•$\overrightarrow{BC}$=0,$\overrightarrow{BC}$=3$\overrightarrow{BD}$,过点D的直线分别交直线AB,AC于点M,N.若$\overrightarrow{AM}$=λ$\overrightarrow{AB}$,$\overrightarrow{AN}$=μ$\overrightarrow{AC}$(λ>0,μ>0),则λ+2μ的最小值是$\frac{8}{3}$.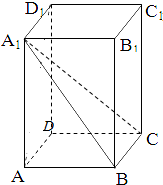 如图,在长方体ABCD-A1B1C1D1中,DA=DC=1,DD1=2,点P在棱CC1上.
如图,在长方体ABCD-A1B1C1D1中,DA=DC=1,DD1=2,点P在棱CC1上.