题目内容
14. 如图,A、B是圆O上的两点,∠AOB=120°,C是AB弧的中点.
如图,A、B是圆O上的两点,∠AOB=120°,C是AB弧的中点.(1)求证:AB平分∠OAC;
(2)延长OA至P使得OA=AP,连接PC,若圆O的半径R=1,求PC的长.
分析 (1)连接OC,证明OA=AC=BC=OB,得到四边形AOBC是菱形,推出AB平分∠OAC.
(2)连接OC,通过判断三角形OPC是直角三角形,然后求解PC.
解答 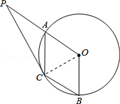 解:(1)证明:连接OC,∵∠AOB=120°,C是AB弧的中点,∴∠AOC=∠BOC=60°,
解:(1)证明:连接OC,∵∠AOB=120°,C是AB弧的中点,∴∠AOC=∠BOC=60°,
∵OA=OC,∴△ACO是等边三角形,∴OA=AC,同理OB=BC,
∴OA=AC=BC=OB,∴四边形AOBC是菱形,∴AB平分∠OAC;…(5分)
(2)解:连接OC,∵C为弧AB中点,∠AOB=120°,∴∠AOC=60°,
∵OA=OC,∴OAC是等边三角形,
∵OA=AC,∴AP=AC,∴∠APC=30°,
∴△OPC是直角三角形,PC=$\sqrt{3}OC=\sqrt{3}$.…(10分)
点评 本题考查直线与圆的位置关系的应用,证明菱形的方法,三角形的边长的求法,考查逻辑推理能力.

练习册系列答案
 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案
相关题目
4.已知x、y∈R,不等式组$\left\{\begin{array}{l}x+2y≥0\\ x-y≤0\\ 0≤y≤k\end{array}\right.$所表示的平面区域的面积为6,则实数k的值为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
3.直线y=-2x+2恰好经过椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1的右焦点和上顶点,则椭圆的离心率等于( )
| A. | $\frac{\sqrt{5}}{5}$ | B. | $\frac{1}{2}$ | C. | $\frac{2\sqrt{5}}{5}$ | D. | $\frac{\sqrt{5}}{2}$ |
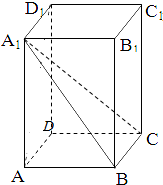 如图,在长方体ABCD-A1B1C1D1中,DA=DC=1,DD1=2,点P在棱CC1上.
如图,在长方体ABCD-A1B1C1D1中,DA=DC=1,DD1=2,点P在棱CC1上.