题目内容
(13分)在平面直角坐标系xOy中,点P到两点 的距离之和等于4,设点P的轨迹为C。
的距离之和等于4,设点P的轨迹为C。
(1)求出C的轨迹方程;
(2)设直线 与C交于A、B两点,k为何值时
与C交于A、B两点,k为何值时 ?
?
 的距离之和等于4,设点P的轨迹为C。
的距离之和等于4,设点P的轨迹为C。(1)求出C的轨迹方程;
(2)设直线
 与C交于A、B两点,k为何值时
与C交于A、B两点,k为何值时 ?
? (1)
(2)

(2)

本试题主要是考查了椭圆的方程的求解,以及直线与椭圆的位置关系的综合运用。
(1)因为点P到两点 的距离之和等于4,设点P的轨迹为C。
的距离之和等于4,设点P的轨迹为C。
符合椭圆的定义,因此可知a,c的值得到椭圆的方程。
(2)设直线与椭圆方程联立方程组,然后结合韦达定理得到根与系数的关系,进而得到k的值。
解:(1) ……(5分)
……(5分)
(2)设
由 得
得 ,
, 恒成立
恒成立




∴当 时
时 ……(13分)
……(13分)
(1)因为点P到两点
 的距离之和等于4,设点P的轨迹为C。
的距离之和等于4,设点P的轨迹为C。符合椭圆的定义,因此可知a,c的值得到椭圆的方程。
(2)设直线与椭圆方程联立方程组,然后结合韦达定理得到根与系数的关系,进而得到k的值。
解:(1)
 ……(5分)
……(5分)(2)设

由
 得
得 ,
, 恒成立
恒成立



∴当
 时
时 ……(13分)
……(13分)
练习册系列答案
 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
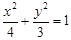 的左、右焦点分别为
的左、右焦点分别为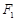 、
、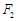 ,直线
,直线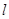 经过点
经过点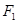 与椭圆交于
与椭圆交于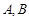 两点。
两点。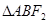 的周长;
的周长;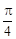 ,求
,求
 的离心率为
的离心率为 =
= ,点
,点 是椭圆上的一点,且点
是椭圆上的一点,且点 两焦点的距离之和为4.
两焦点的距离之和为4.
 关于直线
关于直线 的对称点为
的对称点为 ,求
,求 的取值范围.
的取值范围. 上一点M到直线x+2y-10=0的距离的最小值为( )
上一点M到直线x+2y-10=0的距离的最小值为( )
 上一点P向x轴作垂线,垂足恰为左焦点F1,又点A是椭圆与x轴正半轴的交点,点B是椭圆与y轴正半轴的交点,且AB//OP,
上一点P向x轴作垂线,垂足恰为左焦点F1,又点A是椭圆与x轴正半轴的交点,点B是椭圆与y轴正半轴的交点,且AB//OP, ,求椭圆的方程
,求椭圆的方程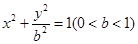 的左焦点为F,左右顶点分别为A,C上顶点为B,过F,B,C三点作
的左焦点为F,左右顶点分别为A,C上顶点为B,过F,B,C三点作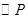 ,其中圆心P的坐标为
,其中圆心P的坐标为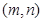 .(1) 若FC是
.(1) 若FC是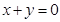 上,求椭圆的方程.
上,求椭圆的方程. 是把坐标平面上的点的横坐标伸长为原来的4倍,纵坐标伸长为原来的3倍的伸压变换,则圆
是把坐标平面上的点的横坐标伸长为原来的4倍,纵坐标伸长为原来的3倍的伸压变换,则圆 在
在 上一点
上一点 到右准线的距离为
到右准线的距离为 ,则该点到左焦点的距离为( )
,则该点到左焦点的距离为( ) 



 与双曲线
与双曲线 有相同的焦点, 则m的值为( )
有相同的焦点, 则m的值为( )


