题目内容
已知数列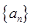 是首项为1,公差为
是首项为1,公差为 的等差数列,数列
的等差数列,数列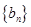 是首项为1,公比为
是首项为1,公比为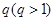 的等比数列.
的等比数列.
(1)若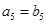 ,
,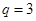 ,求数列
,求数列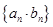 的前
的前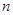 项和;
项和;
(2)若存在正整数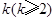 ,使得
,使得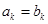 .试比较
.试比较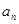 与
与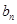 的大小,并说明理由.
的大小,并说明理由.
(1)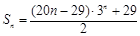
(2)当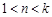 时,
时,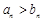 ;当
;当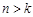 时,
时,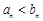 ;当
;当 时,
时,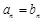 .
.
解析试题分析:解:(1)依题意,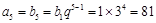 ,
,
故 ,
,
所以 , 3分
, 3分
令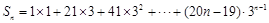 , ①
, ①
则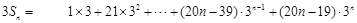 ,②
,②
①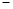 ②得,
②得, ,
,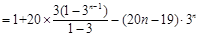
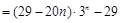 ,
,
所以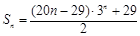 . 7分
. 7分
(2)因为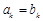 ,
,
所以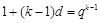 ,即
,即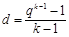 ,
,
故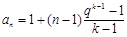 ,
,
又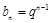 , 9分
, 9分
所以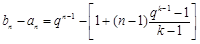
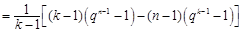
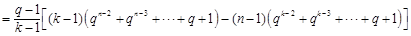
11分
(ⅰ)当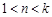 时,由
时,由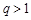 知
知
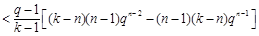
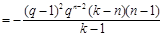
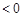 , 13分
, 13分
(ⅱ)当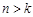 时,由
时,由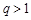 知
知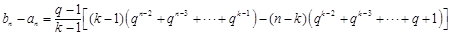
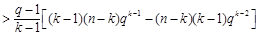
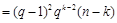
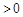 ,
,
综上所述,当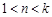 时,
时,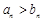 ;当
;当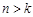 时,
时,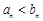 ;当
;当 时,
时,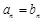 .
.
16分
(注:仅给出“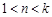 时,
时,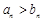 ;
;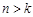 时,
时,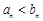 ”得2分.)
”得2分.)
考点:数列的求和
点评:主要是考查了等比数列的求和公司以及数列的单调性的运用,属于中档题。

练习册系列答案
相关题目
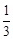 .
.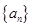 单调递增,
单调递增,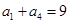 ,
,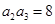 ,
,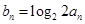
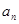 ;
;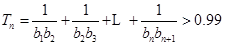 ,求
,求 的最小值
的最小值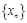 ,
, 满足
满足 ,
,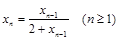 ,
, 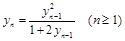 .证明对于任意的自然数n,都存在自然数
.证明对于任意的自然数n,都存在自然数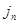 ,使得
,使得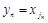 .
. 是函数
是函数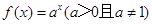 的图象上一点,数列
的图象上一点,数列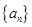 的前n项和
的前n项和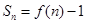 .
.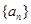 中,
中,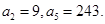
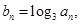 求数列{
求数列{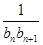 }的前
}的前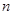 项和
项和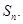
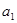 =2,点(
=2,点(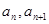 )在函数
)在函数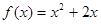 的图像上,其中
的图像上,其中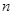 =
=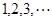 .
. }是等比数列;
}是等比数列;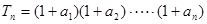 ,求
,求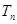 及数列{
及数列{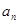 }的通项公式;
}的通项公式;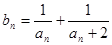 ,求数列{
,求数列{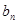 }的前n项和
}的前n项和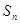 ,并求
,并求 的值.
的值. 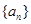 为等差数列,
为等差数列,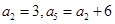 ,数列
,数列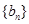 满足
满足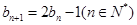 ,且
,且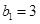 .(1)求通项公式
.(1)求通项公式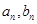 ;(2)设数列
;(2)设数列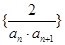 的前
的前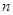 项和为
项和为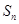 ,试比较
,试比较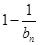 的大小.
的大小.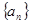 中,
中, 为常数,
为常数, ,且
,且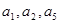 成公比不等于1的等比数列.
成公比不等于1的等比数列.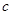 的值;
的值;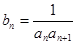 ,求数列
,求数列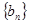 的前
的前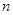 项和
项和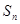 。
。