题目内容
选修4-5:不等式选讲(本小题满分10分)
已知实数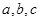 满足
满足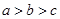 ,且
,且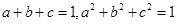 ,求证:
,求证: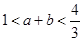
已知实数
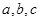 满足
满足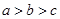 ,且
,且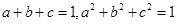 ,求证:
,求证: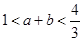
见解析。
本试题主要是考查了不等式的证明,利用均值不等式和消元的思想,表示参数,然后结合a,b是方程x2-(1-c)x+c2-c=0的两个不等实根,得到判别式大于零,得到c的范围。
因为a+b=1-c,ab=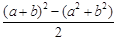 =c2-c, ………………………3分
=c2-c, ………………………3分
所以a,b是方程x2-(1-c)x+c2-c=0的两个不等实根,
则△=(1-c)2-4(c2-c)>0,得-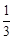 <c<1, ………………………5分
<c<1, ………………………5分
而(c-a)(c-b)=c2-(a+b)c+ab>0,
即c2-(1-c)c+c2-c>0,得c<0,或c>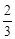 , …………………………8分
, …………………………8分
又因为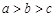 ,所以
,所以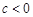 .所以-
.所以-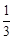 <c<0,即1<a+b<
<c<0,即1<a+b<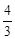 . …………10分
. …………10分
因为a+b=1-c,ab=
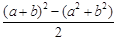 =c2-c, ………………………3分
=c2-c, ………………………3分所以a,b是方程x2-(1-c)x+c2-c=0的两个不等实根,
则△=(1-c)2-4(c2-c)>0,得-
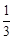 <c<1, ………………………5分
<c<1, ………………………5分而(c-a)(c-b)=c2-(a+b)c+ab>0,
即c2-(1-c)c+c2-c>0,得c<0,或c>
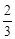 , …………………………8分
, …………………………8分又因为
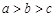 ,所以
,所以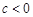 .所以-
.所以-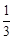 <c<0,即1<a+b<
<c<0,即1<a+b<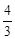 . …………10分
. …………10分
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 .
. 求
求 的单调区间及
的单调区间及 与
与 的大小.
的大小. ,并证明你的结论.
,并证明你的结论.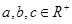 ,求证:
,求证: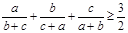 .
. ,判断
,判断 与
与 的大小,并证明你的结论.
的大小,并证明你的结论.
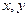 都是正实数,求证:
都是正实数,求证: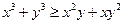 ;
;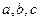 都是正实数,求证:
都是正实数,求证: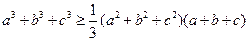 .
.  ≥
≥ .
. 的不等式
的不等式 高
高