题目内容
 .
.(1)若
 求
求 的单调区间及
的单调区间及 的最小值;
的最小值;(2)试比较
 与
与 的大小.
的大小. ,并证明你的结论.
,并证明你的结论.(1)函数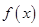 的单调减区间为
的单调减区间为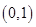 ,单调增区间为
,单调增区间为 ,函数
,函数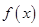 的最小值为
的最小值为 ;
;
(2)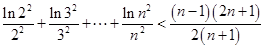 .
.
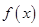 的单调减区间为
的单调减区间为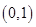 ,单调增区间为
,单调增区间为 ,函数
,函数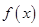 的最小值为
的最小值为 ;
;(2)
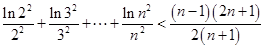 .
.试题分析:(1)先将
 代入函数解析式,并将函数
代入函数解析式,并将函数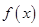 的解析式表示为分段函数,然后求出对应定义域上的单调区间,并求出相应的最小值;(2)利用(1)的结论证明
的解析式表示为分段函数,然后求出对应定义域上的单调区间,并求出相应的最小值;(2)利用(1)的结论证明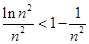 ,再利用放缩法得到
,再利用放缩法得到 ,最后借助同向不等式具备相加性以及累加法得到
,最后借助同向不等式具备相加性以及累加法得到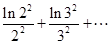
 .
.试题解析:(1)
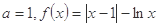
当
 时,
时,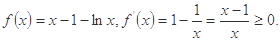
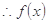 在区间
在区间 上是递增的
上是递增的 当
 时,
时,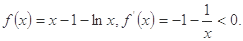
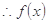 在区间
在区间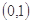 上是递减的.
上是递减的. 故
 时,
时, 的增区间为
的增区间为 ,减区间为
,减区间为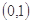 ,
,
(2) 由(1)可知,当
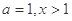 时,有
时,有 即
即
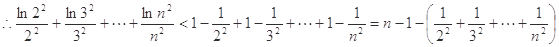
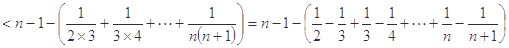
=
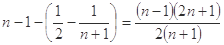 .
. 
练习册系列答案
相关题目
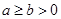 ,求证:
,求证: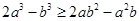 .
.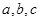 满足
满足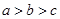 ,且
,且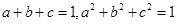 ,求证:
,求证: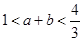
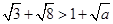 成立的正整数a的最大值是 ( )
成立的正整数a的最大值是 ( ) ,求证:
,求证:
 ,且
,且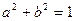 ,
, ,试证:
,试证: 。
。