题目内容
已知函数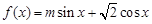 ,
,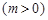 的最大值为2.
的最大值为2.
(1)求函数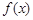 在
在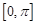 上的值域;
上的值域;
(2)已知 外接圆半径
外接圆半径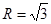 ,
,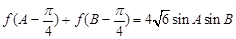 ,角
,角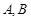 所对的边分别是
所对的边分别是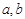 ,求
,求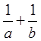 的值.
的值.
(1)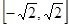 ;(2)
;(2)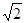 .
.
解析试题分析:(1)根据化一公式可知函数的最大值为 ,其等于2,可以解出
,其等于2,可以解出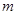 ;函数
;函数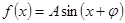 ,由
,由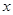 的范围,求出
的范围,求出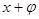 的范围,根据
的范围,根据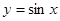 的图像确定函数的值域;
的图像确定函数的值域;
(2)代入(1)的结果可得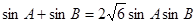 ,根据正弦定理
,根据正弦定理 ,
,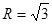 ,可将角化成边,得到关于
,可将角化成边,得到关于 的式子,
的式子,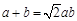 ,两边在同时除以
,两边在同时除以 ,易得结果了.此题属于基础题型.
,易得结果了.此题属于基础题型.
试题解析:(1)由题意,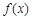 的最大值为
的最大值为 ,所以
,所以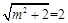 . 2分
. 2分
而 ,于是
,于是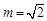 ,
,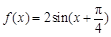 . 4分
. 4分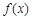 在
在 上递增.在
上递增.在 递减,
递减,
所以函数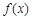 在
在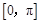 上的值域为
上的值域为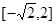 ; 6分
; 6分
(2)化简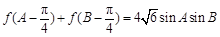 得
得 .
.
由正弦定理,得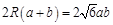 , 9分
, 9分
因为△ABC的外接圆半径为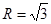 .
.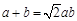 .
.
所以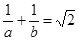 12分
12分
考点:1.三角函数的化简;2.三角函数的性质;2.正弦定理.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
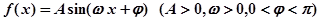 的部分图象,如图所示.
的部分图象,如图所示.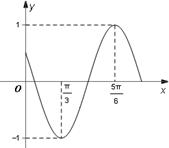
 在
在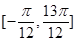 有两个不同的实根,求
有两个不同的实根,求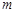 的取值范围.
的取值范围. =
= ,那么sin
,那么sin 的值为 ,cos2
的值为 ,cos2 ,求cosθ的值.
,求cosθ的值.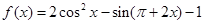 .
.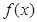 的最小正周期;
的最小正周期;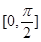 上的最小值和最大值.
上的最小值和最大值.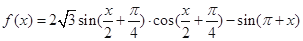 .
. 的最小正周期.
的最小正周期.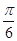 个单位,得到函数
个单位,得到函数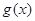 的图象,求函数
的图象,求函数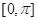 上的值域.
上的值域.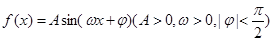 的部分图象如图所示。
的部分图象如图所示。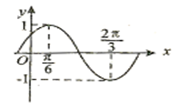
 的最小正周期及解析式;
的最小正周期及解析式;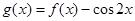 ,求函数
,求函数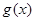 在区间
在区间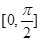 上的最小值.
上的最小值.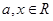 ,函数
,函数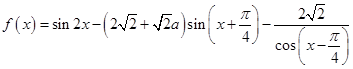 .
.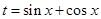 ,将函数
,将函数 表示为关于
表示为关于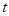 的函数
的函数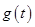 ,求
,求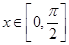 ,不等式
,不等式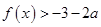 都成立,求实数
都成立,求实数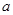 的取值范围.
的取值范围.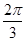 .
. 个单位长度得到,求y=g(x)的单调增区间.
个单位长度得到,求y=g(x)的单调增区间.