题目内容
已知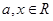 ,函数
,函数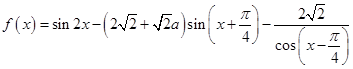 .
.
(1)设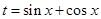 ,将函数
,将函数 表示为关于
表示为关于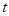 的函数
的函数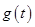 ,求
,求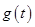 的解析式和定义域;
的解析式和定义域;
(2)对任意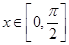 ,不等式
,不等式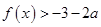 都成立,求实数
都成立,求实数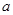 的取值范围.
的取值范围.
(1)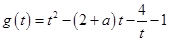 ,定义域为
,定义域为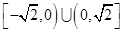 ;(2)实数
;(2)实数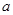 的取值范围是
的取值范围是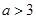 .
.
解析试题分析:(1)由恒等变换公式可求得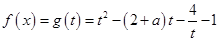 ,并可以表示出定义域;
,并可以表示出定义域;
(2)由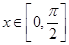 求出
求出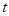 的取值范围,化简成
的取值范围,化简成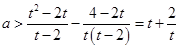 形式,用函数单调性即可求出实数
形式,用函数单调性即可求出实数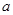 的取值范围.
的取值范围.
试题解析: (1)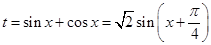
∴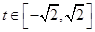 2分
2分
由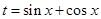 可得
可得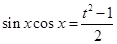 4分
4分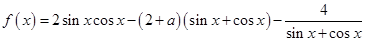
∴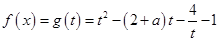 6分
6分
定义域为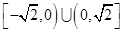 8分
8分
(2) ∵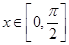
∴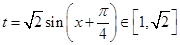 10分
10分
∵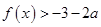 恒成立
恒成立
∴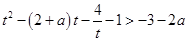 恒成立化简得
恒成立化简得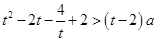
又∵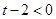
∴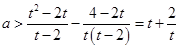 12分
12分
令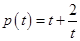 得
得

∴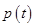 在
在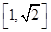 上为减函数14分
上为减函数14分
∴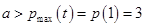
∴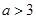 16分
16分
考点:恒等变换公式、恒成立问题.

练习册系列答案
相关题目
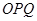 是半径为
是半径为 ,圆心角为
,圆心角为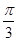 的扇形,
的扇形,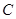 是扇形弧上的动点,
是扇形弧上的动点, 是扇形的内接矩形.记
是扇形的内接矩形.记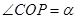 ,求当角
,求当角 取何值时,矩形
取何值时,矩形
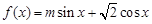 ,
,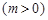 的最大值为2.
的最大值为2.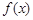 在
在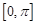 上的值域;
上的值域; 外接圆半径
外接圆半径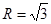 ,
,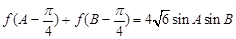 ,角
,角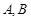 所对的边分别是
所对的边分别是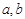 ,求
,求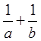 的值.
的值.
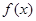 的最小正周期和单调递增区间;
的最小正周期和单调递增区间; 是
是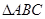 三边长,且
三边长,且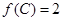 ,
,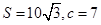 .求角
.求角 及
及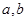 的值.
的值.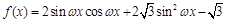 (
(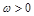 )的最小正周期为
)的最小正周期为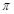 .
. 的单调增区间;
的单调增区间;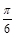 个单位,再向上平移1个单位,得到函数
个单位,再向上平移1个单位,得到函数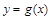 的图象;若
的图象;若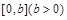 上至少含有10个零点,求b的最小值.
上至少含有10个零点,求b的最小值.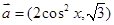 ,
,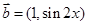 ,函数
,函数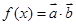 .
. 的最小正周期;
的最小正周期;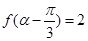 ,
,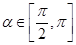 ,求
,求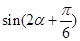 的值.
的值.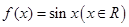 与
与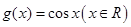 .
.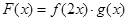 ,有下列结论:①
,有下列结论:①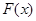 是奇函数;②
是奇函数;②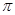 ;③
;③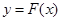 的图象关于点
的图象关于点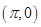 对称;④
对称;④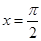 对称.其中正确结论的序号是__________;(直接写出所有正确结论的序号)
对称.其中正确结论的序号是__________;(直接写出所有正确结论的序号)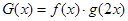 ,求满足
,求满足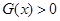 的
的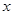 的取值范围;
的取值范围;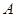 ,函数
,函数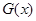 的值域为
的值域为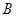 ,试判断集合
,试判断集合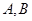 之间的关系.
之间的关系.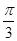 ,回答下列问题.
,回答下列问题.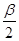 是第几象限的角?
是第几象限的角?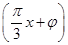 ,x∈R,A>0,0<φ<
,x∈R,A>0,0<φ<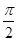 ,y=f(x)的部分图象如图所示,P、Q分别为该图象的最高点和最低点,点P的坐标为(1,A).
,y=f(x)的部分图象如图所示,P、Q分别为该图象的最高点和最低点,点P的坐标为(1,A).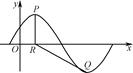
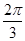 ,求A的值.
,求A的值.