题目内容
(理)已知一组抛物线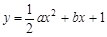
，其中a为2,4,6,8中任取的一个数，b为1,3,5,7中任取的一个数，从这些抛物线中任意抽取两条，它们在与直线x=1交点处的切线相互平行的概率是（ ）
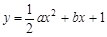，其中a为2,4,6,8中任取的一个数，b为1,3,5,7中任取的一个数，从这些抛物线中任意抽取两条，它们在与直线x=1交点处的切线相互平行的概率是（ ）A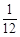． | B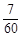． | C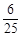． | D． |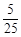
B
解：由题意知，所有抛物线条数是4×4=16条，从16条中任取两条的方法数是
=120，
∵y/=ax+b，
∴在与直线x=1交点处的切线斜率为a+b，
而a为2，4，6，8中任取的一个数，b为1，3，5，7中任取的一个数，保证a+b相等的抛物线对数有14对．
∴它们在与直线x=1交点处的切线相互平行的概率为14/ 120 ="7/" 60 ．
故填：7/ 60 ．
=120，∵y/=ax+b，
∴在与直线x=1交点处的切线斜率为a+b，
而a为2，4，6，8中任取的一个数，b为1，3，5，7中任取的一个数，保证a+b相等的抛物线对数有14对．
∴它们在与直线x=1交点处的切线相互平行的概率为14/ 120 ="7/" 60 ．
故填：7/ 60 ．
练习册系列答案
一线名师口算应用题天天练一本全系列答案
小学学习好帮手系列答案
相关题目
往
走，且只能向右或向下走，随机地选一种走法，则经过点
的概率是（ ）
，比赛采用5局三胜制，则甲打完4局才胜的概率是（ ）
，从｛1，2，3｝中随机选一个数
，则
的概率等于 ．
，试求