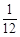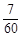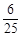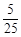题目内容
某单位要在甲、乙、丙、丁4人中安排2人分别担任周六、周日的值班任务(每人被安排是等可能的,每天只安排一人).
(1)共有多少种安排方法?
(2)其中甲、乙两人都被安排的概率是多少?
(3)甲、乙两人中至少有一人被安排的概率是多少?
(1)共有多少种安排方法?
(2)其中甲、乙两人都被安排的概率是多少?
(3)甲、乙两人中至少有一人被安排的概率是多少?
(1)12;(2)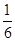 ;(3)
;(3)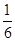 .
.
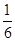 ;(3)
;(3)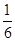 .
.本题是古典概型的概率问题,先列出基本事件总数,再找出满足条件的基本事件的个数,由古典概型的概率公式P= 可求得其概率.对于含有至少或至多的问题也可考虑其对立事件.
可求得其概率.对于含有至少或至多的问题也可考虑其对立事件.
解:(1)安排情况如下:
甲乙,甲丙,甲丁,乙甲,乙丙,乙丁,丙甲,丙乙,丙丁,丁甲,丁乙,丁丙.
∴共有12种安排方法.
(2)甲、乙两人都被安排的情况包括:
“甲乙”,“乙甲”两种,
∴甲、乙两人都被安排(记为事件A)的概率:
P(A)=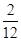 =
=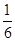 .
.
(3)“甲、乙两人中至少有一人被安排”与“甲、乙两人都不被安排”这两个事件是对立事件,
∵甲、乙两人都不被安排的情况包括:“丙丁”,“丁丙”两种,则“甲、乙两人都不被安排”的概率为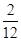 =
=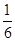 ,
,
∴甲、乙两人中至少有一人被安排(记为事件B)的概率P(B)=1-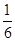 =
=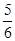
 可求得其概率.对于含有至少或至多的问题也可考虑其对立事件.
可求得其概率.对于含有至少或至多的问题也可考虑其对立事件.解:(1)安排情况如下:
甲乙,甲丙,甲丁,乙甲,乙丙,乙丁,丙甲,丙乙,丙丁,丁甲,丁乙,丁丙.
∴共有12种安排方法.
(2)甲、乙两人都被安排的情况包括:
“甲乙”,“乙甲”两种,
∴甲、乙两人都被安排(记为事件A)的概率:
P(A)=
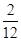 =
=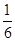 .
.(3)“甲、乙两人中至少有一人被安排”与“甲、乙两人都不被安排”这两个事件是对立事件,
∵甲、乙两人都不被安排的情况包括:“丙丁”,“丁丙”两种,则“甲、乙两人都不被安排”的概率为
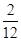 =
=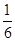 ,
,∴甲、乙两人中至少有一人被安排(记为事件B)的概率P(B)=1-
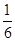 =
=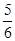

练习册系列答案
相关题目




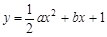 ,其中a为2,4,6,8中任取的一个数,b为1,3,5,7中任取的一个数,从这些抛物线中任意抽取两条,它们在与直线x=1交点处的切线相互平行的概率是( )
,其中a为2,4,6,8中任取的一个数,b为1,3,5,7中任取的一个数,从这些抛物线中任意抽取两条,它们在与直线x=1交点处的切线相互平行的概率是( )