题目内容
同学4人各写一张贺卡,先集中起来,然后每人从中任取一张贺卡;求下列条件的概率:
(1) 每人拿到的1张贺卡都是自己写的概率;
(2) 有且只有1个人拿到的贺卡是自己写的概率
(1) 每人拿到的1张贺卡都是自己写的概率;
(2) 有且只有1个人拿到的贺卡是自己写的概率
解:因为4张贺卡分给4个人,则所有的情况有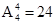 种,而每人都拿到的一张贺卡是自己的只有一种,则利用古典概型可知概率为
种,而每人都拿到的一张贺卡是自己的只有一种,则利用古典概型可知概率为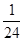
[2] 因为4张贺卡分给4个人,则所有的情况有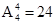 种,而有且只有1个人拿到的贺卡是自己写的情况共有
种,而有且只有1个人拿到的贺卡是自己写的情况共有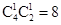 ,则利用古典概型可知概率为
,则利用古典概型可知概率为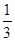
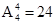 种,而每人都拿到的一张贺卡是自己的只有一种,则利用古典概型可知概率为
种,而每人都拿到的一张贺卡是自己的只有一种,则利用古典概型可知概率为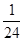
[2] 因为4张贺卡分给4个人,则所有的情况有
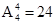 种,而有且只有1个人拿到的贺卡是自己写的情况共有
种,而有且只有1个人拿到的贺卡是自己写的情况共有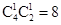 ,则利用古典概型可知概率为
,则利用古典概型可知概率为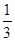
本试题主要考查了古典概型的运用。解决该试题的关键是理解一次试验的所有基本事件数,然后结合事件A发生的事件数,利用比值可以得到概率值。

练习册系列答案
相关题目
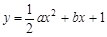 ,其中a为2,4,6,8中任取的一个数,b为1,3,5,7中任取的一个数,从这些抛物线中任意抽取两条,它们在与直线x=1交点处的切线相互平行的概率是( )
,其中a为2,4,6,8中任取的一个数,b为1,3,5,7中任取的一个数,从这些抛物线中任意抽取两条,它们在与直线x=1交点处的切线相互平行的概率是( )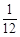
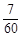
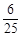
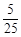
 ,第二次出现的点数为
,第二次出现的点数为 .则事件“
.则事件“ ”的概率为( )
”的概率为( )



 ,则总体中的个体数为( )
,则总体中的个体数为( )
 则
则 三个数从大到小的顺序为________.
三个数从大到小的顺序为________.