题目内容
已知等差数列{an}的前n项和为Sn,且a2=2,S11=66
(1)求{an}的通项公式;
(2)设bn=(
)an.求证:{bn}是等比数列,并求其前n项和Tn.
(1)求{an}的通项公式;
(2)设bn=(
| 1 |
| 4 |
(1)设等差数列{an}的公差为d,
∵a2=a1+d=2,S11=11a1+
d=66,
解得a1=1,d=1,
∴an=n;
(2)由(1)可知,an=n,又bn=(
)an,
∴bn=(
)n,
∴
=
=
,
∴数列{bn}是以b1=
为首项,
为公比的等比数列,
∴数列{bn}的前n项和Tn=
=
(1-(
)n).
∵a2=a1+d=2,S11=11a1+
| 11×10 |
| 2 |
解得a1=1,d=1,
∴an=n;
(2)由(1)可知,an=n,又bn=(
| 1 |
| 4 |
∴bn=(
| 1 |
| 4 |
∴
| bn |
| bn-1 |
(
| ||
(
|
| 1 |
| 4 |
∴数列{bn}是以b1=
| 1 |
| 4 |
| 1 |
| 4 |
∴数列{bn}的前n项和Tn=
| ||||
1-
|
| 1 |
| 3 |
| 1 |
| 4 |

练习册系列答案
相关题目
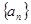 中,
中,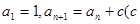 为常数,
为常数,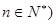 ,且
,且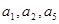 成公比不等于1的等比数列.
成公比不等于1的等比数列.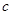 的值;
的值;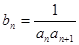 ,求数列
,求数列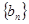 的前
的前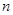 项和
项和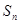
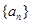 的通项公式
的通项公式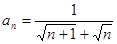 ,它的前n项和为
,它的前n项和为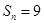 ,则
,则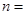 _________.
_________.