题目内容
10.已知圆C过点(-1,0),且圆心在x轴的负半轴上,直线l:y=x+1被该圆所截得的弦长为2$\sqrt{2}$,则过圆心且与直线l平行的直线方程为x-y+3=0.分析 根据题意设圆心C坐标为(x,0),根据圆C过(-1,0),利用两点间的距离公式表示出圆的半径,利用点到直线的距离公式表示出圆心到切线l的距离d,根据已知的弦长,利用垂径定理及勾股定理列出关于x的方程,求出方程的解得到圆心坐标及半径,即可求出过圆心且与直线l平行的直线方程.
解答 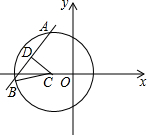 解:设圆心C(x,0),则圆的半径r=|BC|=|x+1|,
解:设圆心C(x,0),则圆的半径r=|BC|=|x+1|,
∴圆心C到直线l的距离|CD|=$\frac{|x+1|}{\sqrt{2}}$,弦长|AB|=2$\sqrt{2}$,
则r=$\sqrt{\frac{(x+1)^{2}}{2}+2}$=|x+1|,
整理得:x=1(不合题意,舍去)或x=-3,
∴圆心C(-3,0),半径为2,
则圆C方程为(x+3)2+y2=4.
∴过圆心且与直线l平行的直线方程为y=x+3,即x-y+3=0.
故答案为:x-y+3=0.
点评 此题考查了直线与圆的位置关系,涉及的知识有:两点间的距离公式,垂径定理,勾股定理,点到直线的距离公式,以及圆的标准方程,熟练掌握公式及定理是解本题的关键.

练习册系列答案
相关题目
20.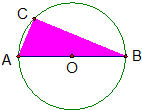 如图,点C为半径是1的圆上一点,且劣弧长AC是劣弧长CB的一半,假设你在这个图形上随机地撒一粒豆子,则∠ABC及豆子落在阴影区域的概率分别是( )
如图,点C为半径是1的圆上一点,且劣弧长AC是劣弧长CB的一半,假设你在这个图形上随机地撒一粒豆子,则∠ABC及豆子落在阴影区域的概率分别是( )
 如图,点C为半径是1的圆上一点,且劣弧长AC是劣弧长CB的一半,假设你在这个图形上随机地撒一粒豆子,则∠ABC及豆子落在阴影区域的概率分别是( )
如图,点C为半径是1的圆上一点,且劣弧长AC是劣弧长CB的一半,假设你在这个图形上随机地撒一粒豆子,则∠ABC及豆子落在阴影区域的概率分别是( )| A. | $\frac{π}{6}$,$\frac{\sqrt{3}}{2π}$ | B. | $\frac{π}{3}$,$\frac{\sqrt{3}}{2π}$ | C. | $\frac{π}{6}$,$\frac{\sqrt{3}}{2}$ | D. | $\frac{π}{6}$,$\frac{3}{2π}$ |
18.已知a,b∈R,i是虚数单位,若a+i与2+bi互为共轭复数,则在复平面内,复数z=$\frac{a+bi}{1+i}$所对应的点在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
5.已知i是虚数单位,m是实数,若$\frac{m+i}{2-i}$是纯虚数,则m=( )
| A. | -2 | B. | -$\frac{1}{2}$ | C. | 2 | D. | $\frac{1}{2}$ |
15.已知|$\overrightarrow{a}$|=1,|$\overrightarrow{b}$|=$\sqrt{2}$,|$\overrightarrow{a}$-2$\overrightarrow{b}$|=$\sqrt{5}$,则向量$\overrightarrow{a}$,$\overrightarrow{b}$的夹角为( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{2}$ |
19.函数f(x)=|x+1|+|x-a|,若不等式f(x)≥6的解集为(-∞,-2]∪[4,+∞),则实数a的值为( )
| A. | -3 | B. | $\sqrt{3}$ | C. | 3 | D. | $-\sqrt{3}$ |