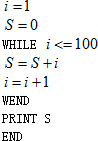题目内容
18.已知a,b∈R,i是虚数单位,若a+i与2+bi互为共轭复数,则在复平面内,复数z=$\frac{a+bi}{1+i}$所对应的点在( )| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
分析 利用共轭复数的概念求得a,b,代入z=$\frac{a+bi}{1+i}$,再由复数代数形式的乘除运算化简,求出z的坐标得答案.
解答 解:∵a+i与2+bi互为共轭复数,
∴a=2,b=-1,
则z=$\frac{a+bi}{1+i}$=$\frac{2-i}{1+i}=\frac{(2-i)(1-i)}{(1+i)(1-i)}=\frac{1-3i}{2}=\frac{1}{2}-\frac{3}{2}i$,
z所对应点的坐标为($\frac{1}{2},-\frac{3}{2}$),位于第四象限.
故选:D.
点评 本题考查复数代数形式的乘除运算,考查了复数的基本概念,是基础题.

练习册系列答案
相关题目
9.下列函数中,为偶函数的是( )
| A. | f(x)=x | B. | f(x)=sinx | C. | f(x)=$\frac{1}{x}$ | D. | f(x)=x2 |
7.函数y=sinx的图象( )
| A. | 关于点$({\frac{π}{2},1})$对称 | B. | 关于直线x=π对称 | C. | 关于点(π,0)对称 | D. | 关于y轴对称 |