Question

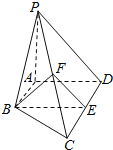
【题目】如图,在四棱锥中,,,平面底面,,和分别是和的中点,求证:

(1)底面;

(2)平面平面;

(3)平面平面.

Answer 1

【答案】(1)证明见解析;(2)证明见解析;(3)证明见解析.

【解析】

（1）平面底面，由此能证明底面；

（2）由已知得是平行四边形，从而，由三角形中位线定理得，由此能证明平面平面；

（3）由，，得，从而，再推导出，由此能证明平面平面．

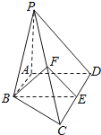
(1)∵平面底面，平面底面，平面，

，

∴底面.

(2)∵是的中点,

∴,且,

∴是平行四边形,

∴,

∵平面,平面,

∴平面,

∵和分别是和的中点,

∴,

∵平面,平面,

∴平面,

∵,

∴平面平面.

(3)∵是平行四边形,

∴ ,

由(1)知底面,

∴,

∴平面,

∴,

∵和分别是和的中点,

∴,

∴,

∴平面,

∵平面,

∴平面 平面.