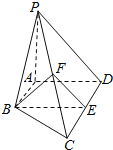
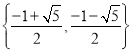��Ŀ����
����Ŀ��ij��ҵ����һ�ֲ�Ʒ���������Է�Ϊ��ָ�겻С��90Ϊһ��Ʒ����С��80С��90Ϊ����Ʒ��С��80Ϊ����Ʒ��ÿ��һ��Ʒӯ��50Ԫ��ÿ������Ʒӯ��30Ԫ��ÿ������Ʒ����10Ԫ.�ֶ�ѧͽ������ʽ�����������IJ�Ʒ��100���ļ����ͳ�����£�

�����ϱ�ͳ�Ƶõ��ס���������Ʒ�ȼ���Ƶ�ʷֱ����Ϊ����������Ʒ�ȼ��ĸ���.
�����������������Ʒ�ĸ��ʣ�
�������������һ����Ʒ��ӯ����С��30Ԫ�ĸ��ʣ�
�������ס���һ��������Ʒ�ֱ�Ϊ30����40�������Ƽס�������һ�칲Ϊ��ҵ���ն���Ԫ��
���𰸡�(��)![]() ��(��)
��(��)![]() ��(��)2000Ԫ.
��(��)2000Ԫ.
��������
���������
(��)������ɵã�����������Ʒ�IJ���ָ��С��80���ݴ˽�Ϲŵ���ͼ��㹫ʽ�ɵ�![]() .
.
(��)������ɵã�������һ����Ʒ�IJ���ָ�겻С��80���ݴ˽�Ϲŵ���ͼ��㹫ʽ�ɵ�![]() .
.
(��)�������Ϲŵ���ͼ��㹫ʽ�ɵü���������Ʒ������Ʒһ��Ʒ�ļ���Ϊ6��21,3������������Ʒ������Ʒһ��Ʒ�ļ���Ϊ4,24,12���ݴ˹��ƿɵüס�������һ�칲Ϊ��ҵ����2000Ԫ.
���������
���������⣬����������Ʒ����Ϊ����ָ��С��80��
���������![]() .
.
���������⣬������һ����Ʒ��ӯ����С��30Ԫ����Ϊ����ָ�겻С��80��
���������![]() .
.
����һ������30����Ʒ�����У�
����Ʒ�ļ���Ϊ![]() ��
��
����Ʒ�ļ���Ϊ![]() ��
��
һ��Ʒ�ļ���Ϊ![]() ��
��
��һ������40����Ʒ�����У�
����Ʒ�ļ���Ϊ![]() ��
��
����Ʒ�ļ���Ϊ![]() ��
��
һ��Ʒ�ļ���Ϊ![]() .
.
��![]() .
.
����Ƽס�������һ�칲Ϊ��ҵ����2000Ԫ.