题目内容
山东省某示范性高中为了推进新课程改革,满足不同层次学生的需求,决定从高一年级开始,在每周的周一、周三、周五的课外活动期间同时开设数学、物理、化学、生物和信息技术辅导讲座,每位有兴趣的同学可以在期间的任何一天参加任何一门科目的辅导讲座,也可以放弃任何一门科目的辅导讲座.(规定:各科达到预先设定的人数时称为满座,否则称为不满座)统计数据表明,各学科讲座各天的满座概率如下表:
| | 信息技术 | 生物 | 化学 | 物理 | 数学 |
| 周一 | 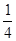 | 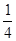 | 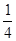 | 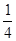 |  |
| 周三 |  |  |  |  | 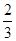 |
| 周五 |  |  |  |  | 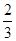 |
(Ⅱ)设周三各辅导讲座满座的科目数为
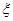 ,求随即变量
,求随即变量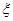 的分布列和数学期望.
的分布列和数学期望.
(1)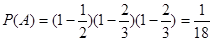 ;
;
(2)分布列为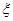
0 1 2 3 4 5 P 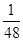
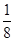
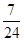
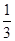
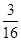
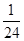
 =
= 。
。
解析试题分析:(1)设数学辅导讲座在周一、周三、周五都不满座为事件A,则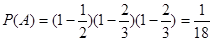 -3分
-3分
(2)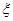 可能取值为0,1,2,3,4,5
可能取值为0,1,2,3,4,5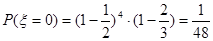 ,
,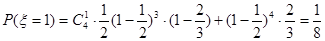 .
.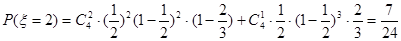 .
.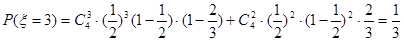 .
.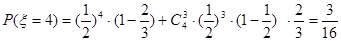 .
.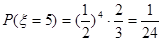 .
.
分布列为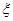
0 1 2 3 4 5 P 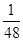
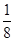
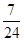
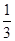
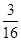
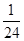
 =
= -----------12分
-----------12分
考点:随机变量的分布列及数学期望
点评:中档题,本题较为典型,背景贴近学生,是随机变量的分布列及数学期望问题的常见题型,解题的关键是理解概率的计算方法。本题对计算能力要求较高。

练习册系列答案
相关题目
“中国式过马路”存在很大的交通安全隐患.某调查机构为了解路人对“中国式过马路”的态度是否与性别有关,从马路旁随机抽取30名路人进行了问卷调查,得到了如下列联表:
| | 男性 | 女性 | 合计 |
| 反感 | 10 | | |
| 不反感 | | 8 | |
| 合计 | | | 30 |
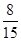 .
.(Ⅰ)请将上面的列联表补充完整(在答题卡上直接填写结果,不需要写求解过程),并据此资料分析反感“中国式过马路 ”与性别是否有关?
(Ⅱ)若从这30人中的女性路人中随机抽取2人参加一活动,记反感“中国式过马路”的人数为X,求X的分布列和数学期望.
| P(K2>k) | 0.05 | 0.025 | 0.010 | 0.005 |
| k | 3.841 | 5.024 | 6.635 | 7.879 |
(参考公式:K2=
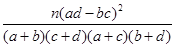 ,其中n="a+b+c+d)"
,其中n="a+b+c+d)" 为了考察某种中药预防流感效果,抽样调查40人,得到如下数据:服用中药的有20人,其中患流感的有2人,而未服用中药的20人中,患流感的有8人。
(1)根据以上数据建立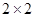 列联表;
列联表;
(2)能否在犯错误不超过0.05的前提下认为该药物有效?
参考
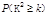 | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
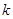 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
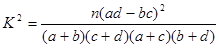 (
(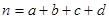 )
) 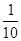 ,不堵车的概率为
,不堵车的概率为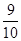 ;走公路Ⅱ堵车的概率为
;走公路Ⅱ堵车的概率为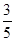 ,不堵车的概率为
,不堵车的概率为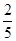 ,若甲、乙两辆汽车走公路Ⅰ,第三辆汽车丙由于其他原因走公路Ⅱ运送水果,且三辆汽车是否堵车相互之间没有影响.
,若甲、乙两辆汽车走公路Ⅰ,第三辆汽车丙由于其他原因走公路Ⅱ运送水果,且三辆汽车是否堵车相互之间没有影响. ,得到黑球或黄球的概率是
,得到黑球或黄球的概率是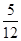 ,得到黄球或绿球的概率是
,得到黄球或绿球的概率是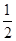 ,试求得到黑球、黄球、绿球的概率各是多少?
,试求得到黑球、黄球、绿球的概率各是多少?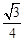 );
);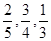 ,且假设各自能否被选中是无关的.
,且假设各自能否被选中是无关的.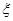 ,试求
,试求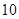 道题中,甲答对其中每道题的概率都是
道题中,甲答对其中每道题的概率都是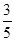 ,乙能答对其中的
,乙能答对其中的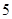 道题.规定每次考试都从备选的
道题.规定每次考试都从备选的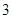 道题进行测试,答对一题加
道题进行测试,答对一题加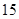 分才能入选.
分才能入选.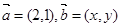
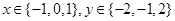 ,求向量
,求向量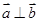 的概率;
的概率;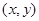 构成区域
构成区域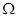 :
: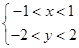 ,求二元数组
,求二元数组
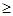 1的概率.
1的概率.