题目内容
(12分)设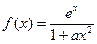 ,其中
,其中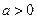 .
.
(1)当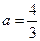 时,求
时,求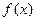 的极值点;
的极值点;
(2)若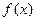 为R上的单调函数,求
为R上的单调函数,求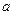 的取值范围.
的取值范围.
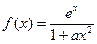 ,其中
,其中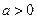 .
.(1)当
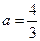 时,求
时,求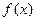 的极值点;
的极值点;(2)若
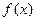 为R上的单调函数,求
为R上的单调函数,求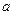 的取值范围.
的取值范围.对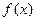 求导得
求导得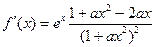 ①
①
(1)当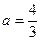 时,若
时,若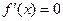 ,则
,则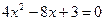 ,解得
,解得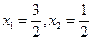
结合①,可知
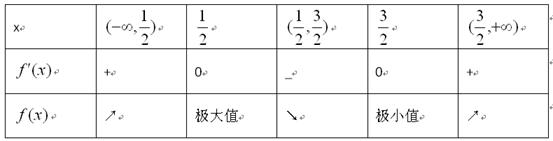
所以,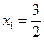 是极小值点,
是极小值点,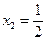 是极大值点.------------------6分
是极大值点.------------------6分
(2)若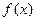 为R上的单调函数,则
为R上的单调函数,则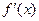 在R上不变号,结合①与条件a>0,知
在R上不变号,结合①与条件a>0,知
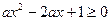 在R上恒成立,因此
在R上恒成立,因此 ,
,
由此并结合a>0,知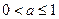 .--------
.-------- ---------12分
---------12分
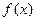 求导得
求导得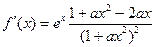 ①
①(1)当
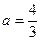 时,若
时,若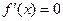 ,则
,则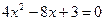 ,解得
,解得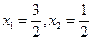
结合①,可知

所以,
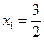 是极小值点,
是极小值点,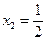 是极大值点.------------------6分
是极大值点.------------------6分(2)若
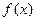 为R上的单调函数,则
为R上的单调函数,则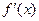 在R上不变号,结合①与条件a>0,知
在R上不变号,结合①与条件a>0,知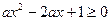 在R上恒成立,因此
在R上恒成立,因此 ,
,由此并结合a>0,知
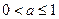 .--------
.-------- ---------12分
---------12分略

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
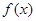 的定义域为
的定义域为 ,
,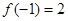 ,对任意
,对任意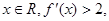 则
则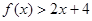
 )
) (-
(-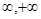 )
)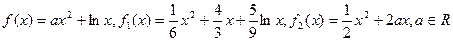 .
.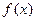 在点
在点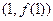 处的切线方程;
处的切线方程;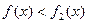 在区间
在区间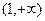 上恒成立,求
上恒成立,求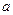 的取值范围;
的取值范围;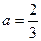 时,求证:在区间
时,求证:在区间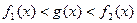 恒成立的函数
恒成立的函数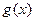 有无穷多个.
有无穷多个.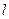 过点
过点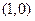 ,且与曲线
,且与曲线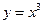 和
和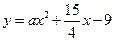 都相切,
都相切,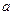 的值。
的值。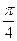 .
. ?若存在,求出最小的正整数k,否则请说明理由.
?若存在,求出最小的正整数k,否则请说明理由.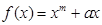 的导函数为
的导函数为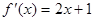 ,则数列
,则数列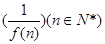 的前
的前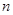 项
项
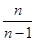


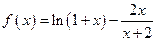 ,证明:当
,证明:当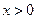 时,
时,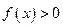
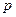 ,证明:
,证明: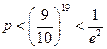
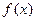 =
=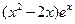 (e为自然对数的底数)
(e为自然对数的底数) 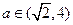 ,求函数
,求函数 ]上的最大值和最小值.(5分)
]上的最大值和最小值.(5分)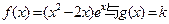 的图象有三个不同的交点,求实数k的取值范围.
的图象有三个不同的交点,求实数k的取值范围. )(2分)
)(2分)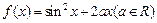 ,若对任意实数
,若对任意实数 ,直线
,直线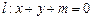 都不是曲线
都不是曲线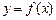 的切线,则
的切线,则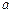 的取值范围是 .
的取值范围是 . 