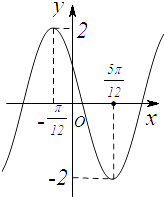题目内容
【题目】已知函数![]() 的图象与
的图象与![]() 轴相切,且切点在
轴相切,且切点在![]() 轴的正半轴上.
轴的正半轴上.
(1)求曲线![]() 与
与![]() 轴,直线
轴,直线![]() 及
及![]() 轴围成图形的面积
轴围成图形的面积![]() ;
;
(2)若函数![]() 在
在![]() 上的极小值不大于
上的极小值不大于![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】试题分析:(1)根据导数的几何意义可得到![]() 得
得![]() ,
, ![]() ,解得
,解得![]() .(2)先求导
.(2)先求导![]() ,研究导函数的正负,当
,研究导函数的正负,当![]() 时,
时, ![]() 无极值;当
无极值;当![]() ,即
,即![]() 时,分析导数的正负使得极值
时,分析导数的正负使得极值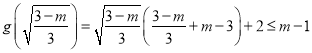 ,解出不等式即可。
,解出不等式即可。
解:(1)![]() ,
, ![]() 得
得![]() ,
,
由题意可得![]() ,解得
,解得![]() .
.
故![]() ,
, 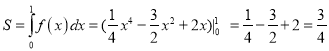 .
.
(2)![]() ,
, ![]()
当![]() 时,
时, ![]() 无极值;
无极值;
当![]() ,即
,即![]() 时,令
时,令![]() 得
得![]() ;
;
令![]() 得
得![]() 或.
或. ![]()
![]() 在
在![]() 处取得极小值,
处取得极小值,
当![]() ,即
,即![]() ,
, ![]() 在(-3,2)上无极小值,
在(-3,2)上无极小值,
故当![]() 时,
时, ![]() 在(-3,2)上有极小值
在(-3,2)上有极小值
且极小值为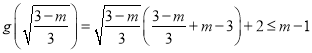 ,
,
即![]() .
.
![]() ,
, ![]() ,
, ![]() .
.
又![]() ,故
,故![]() .
.
点睛:这个题目考查的是利用导数研究函数的极值;求导后出现二次函数形式,一般的讨论方法有:先看二次项系数是否为0,然后看能否因式分解,能分解的话,直接比较两根的大小,不能分解就由判别式和图像结合判断导函数的正负。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】某中学一位高三班主任对本班50名学生学习积极性和对待班级工作的态度进行调查,得到的统计数据如表所示:
积极参加班级工作 | 不积极参加班级工作 | 合计 | |
学习积极性高 | 18 | 7 | 25 |
学习积极性不高 | 6 | 19 | 25 |
合计 | 24 | 26 | 50 |
(1)如果随机调查这个班的一名学生,那么抽到不积极参加班级工作且学习积极性不高的学生的概率是多少?
(2)若不积极参加班级工作且学习积极性高的7名学生中有两名男生,现从中抽取2名学生参加某项活动,问2名学生中有1名男生的概率是多少?
(3)学生的学习积极性与对待班级工作的态度是否有关系?请说明理由.
附:

![]()