题目内容
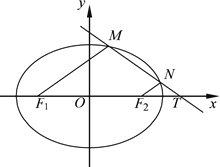
【题目】如图,在平面直角坐标系![]() 中,椭圆
中,椭圆![]() (a>b>0)的左、右焦点分别为
(a>b>0)的左、右焦点分别为![]() ,
,![]() . 已知
. 已知![]() 和
和![]() 都在椭圆上,其中
都在椭圆上,其中![]() 为椭圆的离心率.
为椭圆的离心率.

(1)求椭圆![]() 的标准方程;
的标准方程;
(2)过![]() 作斜率为
作斜率为![]()
![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点(
两点(![]() 点在
点在![]() 点的左侧),且
点的左侧),且![]() . 若
. 若![]() ,求
,求![]() 的值.
的值.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)将![]() 和
和![]() 代入椭圆方程求解即可.
代入椭圆方程求解即可.
(2) 设![]() ,
,![]() ,
,![]() ,联立直线与椭圆的方程,根据
,联立直线与椭圆的方程,根据![]() 可得
可得![]() ,再代入直线方程与韦达定理,再根据
,再代入直线方程与韦达定理,再根据![]() ,所以
,所以![]() 在
在![]() 的中垂线上,进而得出关于
的中垂线上,进而得出关于![]() 的函数解析式,根据坐标求解即可.
的函数解析式,根据坐标求解即可.
(1)因为![]() 和
和![]() 都在椭圆上,所以
都在椭圆上,所以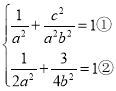
由①式得![]() ,即
,即![]() ,所以
,所以![]() ,代入②式,解得
,代入②式,解得![]() .
.
所以椭圆![]() 的标准方程为
的标准方程为![]() .
.
(2)设![]() ,
,![]() ,因为过
,因为过![]() 作斜率为
作斜率为![]()
![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点,所以
两点,所以![]() .
.
由![]() 得
得![]() ,所以
,所以
思路一:
因为![]() ,
,![]() ,所以
,所以![]() ,
,![]() .
.
因为![]() ,所以
,所以![]() ,即
,即![]() ,
,
整理得![]() ,所以
,所以![]() ,
,
又![]() ,所以
,所以![]() ,
,
即![]() ,
,![]() (*).
(*).
所以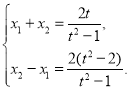 则
则![]() ,所以
,所以![]()
因为![]() ,所以
,所以![]() 在
在![]() 的中垂线上,则
的中垂线上,则![]() .
.
所以![]() ,即
,即![]() ,所以
,所以![]() ,又
,又![]() ,所以
,所以![]() .
.
思路二:
因为![]() ,所以
,所以![]() ,即
,即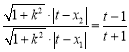 ,所以
,所以![]() ,
,
即![]() ,所以
,所以![]() .
.
因为![]() ,所以
,所以![]() 在
在![]() 的中垂线上,则
的中垂线上,则![]() .所以
.所以![]() ,又
,又![]() ,则
,则![]() .
.
所以 解得
解得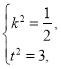 故
故![]() .
.
思路三:
因为![]() ,所以
,所以![]() ,所以
,所以![]() 在
在![]() 的中垂线上,则
的中垂线上,则![]() .
.
因为![]() ,所以
,所以![]() ,则
,则![]() ,所以
,所以![]() 在
在![]() 的中垂线上,则
的中垂线上,则![]() .
.
所以 解得
解得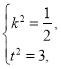 故
故![]() .
.

 中考解读考点精练系列答案
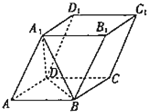
中考解读考点精练系列答案【题目】如图,四棱锥![]() 的底面是菱形,
的底面是菱形,![]() 底面
底面![]() ,
,![]() 分别是
分别是![]() 的中点,
的中点,![]() ,
,![]() ,
,![]() .
.
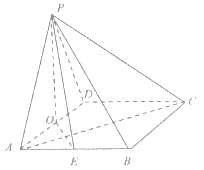
(I)证明:![]() ;
;
(II)求直线![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
(III)在![]() 边上是否存在点
边上是否存在点![]() ,使
,使![]() 与
与![]() 所成角的余弦值为
所成角的余弦值为![]() ,若存在,确定点
,若存在,确定点![]() 位置;若不存在,说明理由.
位置;若不存在,说明理由.
【题目】某大型商场的空调在1月到5月的销售量与月份相关,得到的统计数据如下表:
月份 | 1 | 2 | 3 | 4 | 5 |
销量 | 0.6 | 0.8 | 1.2 | 1.6 | 1.8 |
(1)经分析发现1月到5月的销售量可用线性回归模型拟合该商场空调的月销量![]() (百件)与月份
(百件)与月份![]() 之间的相关关系.请用最小二乘法求
之间的相关关系.请用最小二乘法求![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ,并预测6月份该商场空调的销售量;
,并预测6月份该商场空调的销售量;
(2)若该商场的营销部对空调进行新一轮促销,对7月到12月有购买空调意愿的顾客进行问卷调查.假设该地拟购买空调的消费群体十分庞大,经过营销部调研机构对其中的500名顾客进行了一个抽样调查,得到如下一份频数表:
有购买意愿对应的月份 | 7 | 8 | 9 | 10 | 11 | 12 |
频数 | 60 | 80 | 120 | 130 | 80 | 30 |
现采用分层抽样的方法从购买意愿的月份在7月与12月的这90名顾客中随机抽取6名,再从这6人中随机抽取3人进行跟踪调查,求抽出的3人中恰好有2人是购买意愿的月份是12月的概率.
参考公式与数据:线性回归方程![]() ,其中
,其中 ,
,![]() .
.