��Ŀ����
����Ŀ��ij������ţ����ij̨�豸������A��B��������Ʒ.����1��A��Ʒ����ţ��2�֣�ʹ���豸1Сʱ������1 000Ԫ������1��B��Ʒ����ţ��1.5�֣�ʹ���豸1.5Сʱ������1 200Ԫ.Ҫ��ÿ��B��Ʒ�IJ���������A��Ʒ������2�����豸ÿ������A��B���ֲ�Ʒʱ��֮�Ͳ�����12Сʱ.�ٶ�ÿ��ɻ�ȡ����ţ������W(��λ����)��һ�������������ֲ���Ϊ
W | 12 | 15 | 18 |
P | 0.3 | 0.5 | 0.2 |
�ó�ÿ����ݻ�ȡ����ţ����������������ʹ�����������ÿ���������Z(��λ��Ԫ)��һ���������.
(I)��Z�ķֲ��к;�ֵ��
(II)��ÿ��ɻ�ȡ����ţ���������������3����������1�������������10 000Ԫ�ĸ���.
���𰸡�������![]() �ķֲ���Ϊ��
�ķֲ���Ϊ��
| 8160 | 10200 | 10800 |
| 0��3 | 0��5 | 0��2 |
![]() ��������0��973��
��������0��973��
����������������ÿ��![]() ���ֲ�Ʒ�����������ֱ�Ϊ
���ֲ�Ʒ�����������ֱ�Ϊ![]() ����Ӧ�Ļ���Ϊ
����Ӧ�Ļ���Ϊ![]() ��
��
���� ��1��
��1��

Ŀ�꺯��Ϊ![]() ��
��
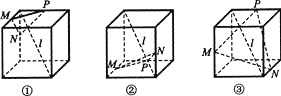
��![]() ʱ����1����ʾ��ƽ��������ͼ1����������ֱ�Ϊ
ʱ����1����ʾ��ƽ��������ͼ1����������ֱ�Ϊ![]() ��
��
��![]() ����Ϊ
����Ϊ![]() ��
��
��![]() ʱ��ֱ��
ʱ��ֱ��![]() ��
��![]() ��
��![]() ���ϵĽؾ����
���ϵĽؾ����
������![]() ��
��
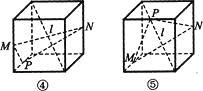
��![]() ʱ����1����ʾ��ƽ��������ͼ2����������ֱ�Ϊ
ʱ����1����ʾ��ƽ��������ͼ2����������ֱ�Ϊ![]() ��
��
��![]() ����Ϊ
����Ϊ![]() ��
��
��![]() ʱ��ֱ��
ʱ��ֱ��![]() ��
��![]() ��
��![]() ���ϵĽؾ����
���ϵĽؾ����
������![]() ��
��
��![]() ʱ����1����ʾ��ƽ��������ͼ3��
ʱ����1����ʾ��ƽ��������ͼ3��
�ĸ�����ֱ�Ϊ![]() ��
��
��![]() ����Ϊ
����Ϊ![]() ��
��
��![]() ʱ��ֱ��
ʱ��ֱ��![]() ��
��![]() ��
��![]() ���ϵĽؾ����
���ϵĽؾ����
������![]() ��
��
��������![]() �ķֲ���Ϊ
�ķֲ���Ϊ
| 8160 | 10200 | 10800 |
| 0��3 | 0��5 | 0��2 |
��ˣ� ![]()
�������ɣ�����֪��һ������������10000Ԫ�ĸ���![]() ��
��
�ɶ���ֲ���3����������1������������10000Ԫ�ĸ���Ϊ![]()

 �¿α�����Ķ�ѵ��ϵ�д�
�¿α�����Ķ�ѵ��ϵ�д�