题目内容
(本题满分14分)
某零售店近五个月的销售额和利润额资料如下表:
| 商店名称 | A | B | C | D | E |
销售额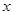 (千万元) (千万元) | 3 | 5 | 6 | 7 | 9 9 |
利润额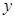 (百万元) (百万元) | 2 | 3 | 3 | 4 | 5 |
(2)用最小二乘法计算利润额
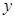 关于销售额
关于销售额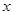 的回归直线方程;
的回归直线方程;(3)当销售额为4(千万元)时,利用(2)的结论估计该零售店的利润额(百万元).
(1) 两个变量呈正线性相关关系
(2)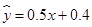
(3) 当销售额为4(千万元)时,可以估计该店的利润额为2.4(百万元).
解析试题分析:解:(1)散点图如下. 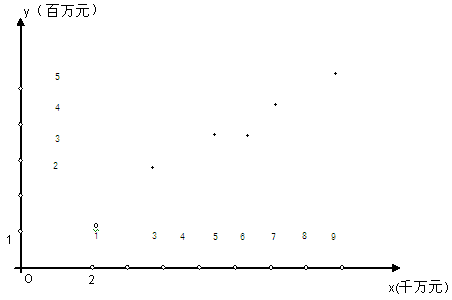
两个变量呈正线性相关关系.
(2)设回归直线的方程是: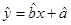 .
.
由题中的数据可知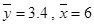 .
.
所以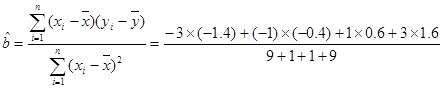
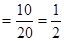 .
.  .
.
所以利润额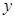 关于销售额
关于销售额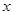 的回归直线方程为
的回归直线方程为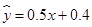 .
.
(3)由(2)知,当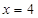 时,
时,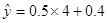 =2.4,
=2.4,
所以当销售额为4(千万元)时,可以估计该店的利润额为2.4(百万元).
考点:散点图以及线性回归方程的求解
点评:解决的关键是利用已知的数据得到系数a,b的值,进而结合实际问题中根据x,求解y的值,属于基础题。

练习册系列答案
相关题目
某学校课题组为了研究学生的数学成绩与物理成绩之间的关系,随机抽取高二年级20名学生某次考试成绩(满分100分)如下表所示:
| 序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 数学成绩 | 95 | 75 | 80 | 94 | 92 | 65 | 67 | 84 | 98 | 71 | 67 | 93 | 64 | 78 | 77 | 90 | 57 | 83 | 72 | 83 |
| 物理成绩 | 90 | 63 | 72 | 87 | 91 | 71 | 58 | 82 | 93 | 81 | 77 | 82 | 48 | 85 | 69 | 91 | 61 | 84 | 78 | 86 |
 (1)根据上表完成下面的2×2列联表(单位:人):
(1)根据上表完成下面的2×2列联表(单位:人):| | 数学成绩优秀 | 数学成绩不优秀 | 合 计 |
| 物理成绩优秀 | | | |
| 物理成绩不优秀 | | | |
| 合 计 | | | 20 |
参考数据:
假设有两个分类变量
 和
和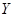 ,它们的值域分别为
,它们的值域分别为 和
和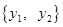 ,其样本频数列联表(称为
,其样本频数列联表(称为 列联表)为:
列联表)为:| | 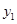 | 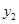 | 合计 |
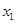 | 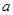 |  | 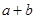 |
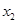 |  | 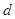 | 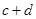 |
| 合计 | 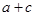 | 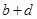 |  |
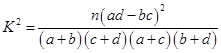 ,其中
,其中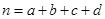 为样本容量;
为样本容量;②独立检验随机变量
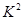 的临界值参考表:
的临界值参考表: | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
通过市场调查,得到某产品的资金投入x(万元)与获得的利润y(万元)的数据,如表所示:
| 资金投入x | 2 | 3 | 4 | 5 | 6 |
| 利润y | 2 | 3 | 5 | 6 | 9 |
(Ⅱ)根据上表提供的数据,用最小二乘法求线性回归直线方程=x+;
(Ⅲ)现投入资金10万元,估计获得的利润为多少万元?
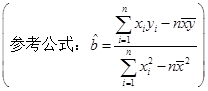
(本题14分)下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量( 吨)与相应的生产能耗
吨)与相应的生产能耗 (吨)标准煤的几组对照数据:
(吨)标准煤的几组对照数据:
 | 3 | 4 | 5 | 6 |
 | 2.5 | 3 | 4 | 4.5 |
(1)请画出上表数据的散点图;并指出x,y 是否线性相关;
(2)请根据上表提供的数据,用最小二乘法求出
 关于
关于 的线性回归方程
的线性回归方程 ;
;(3)已知该厂技术改造前100吨甲产品能耗为90吨标准煤,试根据(2)求出的线性回归方程,预测生产100吨甲产品的生产能耗比技术改造前降低多少吨标准煤?
(参考:用最小二乘法求线性回归方程系数公式
 ,
, )
) 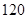 人,其中女性
人,其中女性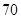 人,男性
人,男性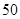 人.女性中有
人.女性中有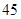 人主要的休闲方式是看电视,另外
人主要的休闲方式是看电视,另外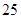 人主要的休闲方式是运动;男性中有
人主要的休闲方式是运动;男性中有 人主要的休闲方式是看电视,另外
人主要的休闲方式是看电视,另外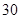 人主要的休闲方式是运动.
人主要的休闲方式是运动.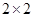 的列联表;
的列联表;

 的分布列及其数学期望。
的分布列及其数学期望。