题目内容
某学校课题组为了研究学生的数学成绩与物理成绩之间的关系,随机抽取高二年级20名学生某次考试成绩(满分100分)如下表所示:
| 序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 数学成绩 | 95 | 75 | 80 | 94 | 92 | 65 | 67 | 84 | 98 | 71 | 67 | 93 | 64 | 78 | 77 | 90 | 57 | 83 | 72 | 83 |
| 物理成绩 | 90 | 63 | 72 | 87 | 91 | 71 | 58 | 82 | 93 | 81 | 77 | 82 | 48 | 85 | 69 | 91 | 61 | 84 | 78 | 86 |
 (1)根据上表完成下面的2×2列联表(单位:人):
(1)根据上表完成下面的2×2列联表(单位:人):| | 数学成绩优秀 | 数学成绩不优秀 | 合 计 |
| 物理成绩优秀 | | | |
| 物理成绩不优秀 | | | |
| 合 计 | | | 20 |
参考数据:
假设有两个分类变量
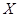 和
和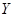 ,它们的值域分别为
,它们的值域分别为 和
和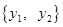 ,其样本频数列联表(称为
,其样本频数列联表(称为 列联表)为:
列联表)为:| | 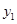 | 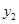 | 合计 |
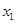 | 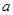 |  | 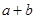 |
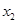 |  | 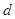 | 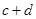 |
| 合计 | 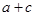 | 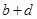 |  |
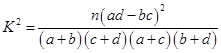 ,其中
,其中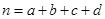 为样本容量;
为样本容量;②独立检验随机变量
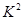 的临界值参考表:
的临界值参考表: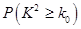 | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(1) 数学成绩优秀 数学成绩不优秀 合 计 物理成绩优秀 5 2 7 物理成绩不优秀 1 12 13 合 计 6 14 20
(2) 有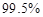 的把握认为:学生的数学成绩与物理成绩之间有关系
的把握认为:学生的数学成绩与物理成绩之间有关系
解析试题分析:(1)解:2×2列联表为(单位:人): 数学成绩优秀 数学成绩不优秀 合 计 物理成绩优秀 5 2 7 物理成绩不优秀 1 12 13 合 计 6 14 20
4分
(2)解:提出假设 :学生数学成绩与物理成绩之间没有关系. 6分
:学生数学成绩与物理成绩之间没有关系. 6分
根据列联表可以求得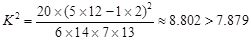 . 9分
. 9分
当 成立时,
成立时,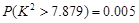 11分
11分
所以我们有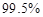 的把握认为:学生的数学成绩与物理成绩之间有关系 12分
的把握认为:学生的数学成绩与物理成绩之间有关系 12分
考点:2×2列联表
点评:解决的关键是利用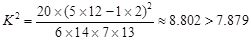 的估计值,来求解运用。属于基础题。
的估计值,来求解运用。属于基础题。

 步步高达标卷系列答案
步步高达标卷系列答案某糖厂为了了解一条自动生产线上袋装白糖的重量,随机抽取了100袋,并称出每袋白糖的重量(单位:g),得到如下频率分布表。
| 分组 | 频数 | 频率 |
| [485.5,490.5) | 10 |  |
| [490.5,495.5) | 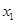 |  |
| [495.5,500.5) | 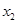 | 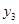 |
| [500.5,505.5] | 10 | |
| 合计 | 100 | |
 ,
, ,
,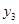 成等差数列。
成等差数列。(I)将有关数据分别填入所给的频率。分布表的所有空格内,并画出频率分布直方图。
(II)在这100包白糖的重量中,估计其中位数。
第 届亚运会于
届亚运会于 年
年 月
月 日至
日至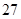 日在中国广州进行,为了做好接待工作,组委会招募了
日在中国广州进行,为了做好接待工作,组委会招募了 名男志愿者和
名男志愿者和 名女志愿者,调查发现,男、女志愿者中分别有
名女志愿者,调查发现,男、女志愿者中分别有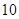 人和
人和 人喜爱运动,其余不喜爱.
人喜爱运动,其余不喜爱.
(1)根据以上数据完成以下 列联表:
列联表:
| | 喜爱运动 | 不喜爱运动 | 总计 |
| 男 | 10 | | 16 |
| 女 | 6 | | 14 |
| 总计 | | | 30 |
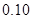 的前提下认为性别与喜爱运动有关?
的前提下认为性别与喜爱运动有关?(3)如果从喜欢运动的女志愿者中(其中恰有
 人会外语),抽取
人会外语),抽取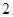 名负责翻译工作,则抽出的志愿者中
名负责翻译工作,则抽出的志愿者中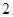 人都能胜任翻译工作的概率是多少?
人都能胜任翻译工作的概率是多少?附:K2=
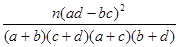
| P(K2≥k) | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| k | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
2012年3月2日,国家环保部发布了新修订的《环境空气质量标准》.其中规定:居民区中的PM2.5(PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称可入肺颗粒物)年平均浓度不得超过35微克/立方米,PM2.5的24小时平均浓度不得超过75微克/立方米. 某城市环保部门随机抽取了一居民区去年40天的PM2.5的24小时平均浓度的监测数据,数据统计如下:
| 组别 | PM2.5(微克/立方米) | 频数(天) | 频率 |
| 第一组 | (0,15] | 4 | 0.1 |
| 第二组 | (15,30] | 12 | 0.3 |
| 第三组 | (30,45] | 8 | 0.2 |
| 第四组 | (45,60] | 8 | 0.2 |
| 第三组 | (60,75] | 4 | 0.1 |
| 第四组 | (75,90) | 4 | 0.1 |
(Ⅱ)求该样本的平均数,并根据样本估计总体的思想,从PM2.5的年平均浓度考虑,判断该居民区的环境是否需要改进?说明理由;
(Ⅲ)将频率视为概率,对于去年的某2天,记这2天中该居民区PM2.5的24小时平均浓度符合环境空气质量标准的天数为
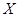 ,求
,求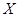 的分布列及数学期望
的分布列及数学期望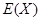 .
. 由于当前学生课业负担较重,造成青少年视力普遍下降,现从某高中随机抽取16名学生,经校医检查得到每个学生的视力状况的茎叶图(以小数点前的一位数字为茎,小数点后的一位数字为叶)如图示:
| | |
| 4 | 3 5 6 6 6 7 7 7 8 8 9 9 |
| 5 | 0 1 1 2 |
| | |
指出这组数据的众数和中位数;
若视力测试结果不低于5.0,则称为“健康视力”,求校医从这16人中随机选取3人,至多有1人是“健康视力”的概率;以这16人的样本数据来估计整个学校的总体数据,若从该校(人数很多)任选3人,记
 表示抽到“健康视力”学生的人数,求
表示抽到“健康视力”学生的人数,求 的分布列及数学期望
的分布列及数学期望 (本题满分14分)
某零售店近五个月的销售额和利润额资料如下表:
| 商店名称 | A | B | C | D | E |
销售额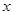 (千万元) (千万元) | 3 | 5 | 6 | 7 | 9 9 |
利润额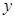 (百万元) (百万元) | 2 | 3 | 3 | 4 | 5 |
(2)用最小二乘法计算利润额
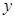 关于销售额
关于销售额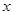 的回归直线方程;
的回归直线方程;(3)当销售额为4(千万元)时,利用(2)的结论估计该零售店的利润额(百万元).
(本小题满分13分)
甲、乙两台机床生产同一型号零件.记生产的零件的尺寸为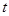 (cm),相关行业质检部门规定:若
(cm),相关行业质检部门规定:若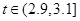 ,则该零件为优等品;若
,则该零件为优等品;若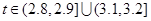 ,则该零件为中等品;其余零件为次品.现分别从甲、乙机床生产的零件中各随机抽取50件,经质量检测得到下表数据:
,则该零件为中等品;其余零件为次品.现分别从甲、乙机床生产的零件中各随机抽取50件,经质量检测得到下表数据:
| 尺寸 | 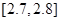 | 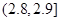 | 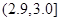 | 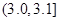 | 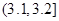 | 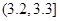 |
| 甲机床零件频数 | 2 | 3 | 20 | 20 | 4 | 1 |
| 乙机床零件频数 | 3 | 5 | 17 | 13 | 8 | 4 |
(Ⅱ)对于这两台机床生产的零件,在排除其它因素影响的情况下,试根据样本估计总体的思想,估计约有多大的把握认为“零件优等与否和所用机床有关”,并说明理由.
参考公式:
 .
.参考数据:
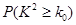 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
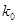 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
(本小题满分12分)
2012年3月2日,国家环保部发布了新修订的《环境空气质量标准》.其中规定:居民区中的PM2.5(PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称可入肺颗粒物)年平均浓度不得超过35微克/立方米,PM2.5的24小时平均浓度不得超过75微克/立方米. 某城市环保部门随机抽取了一居民区去年40天的PM2.5的24小时平均浓度的监测数据,数据统计如下:
| 组别 | PM2.5(微克/立方米) | 频数(天) | 频率 |
| 第一组 | (0,15] | 4 | 0.1 |
| 第二组 | (15,30] | 12 | 0.3 |
| 第三组 | (30,45] | 8 | 0.2 |
| 第四组 | (45,60] | 8 | 0.2 |
| 第三组 | (60,75] | 4 | 0.1 |
| 第四组 | (75,90) | 4 | 0.1 |
(2)求该样本的平均数,并根据样本估计总体的思想,从PM2.5的年平均浓度考虑,判断该居民区的环境是否需要改进?说明理由;
(3)将频率视为概率,对于去年的某2天,记这2天中该居民区PM2.5的24小时平均浓度符合环境空气质量标准的天数为
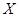 ,求
,求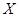 的分布列及数学期望
的分布列及数学期望 .
. 