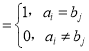题目内容
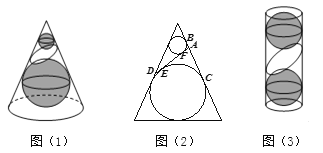
【题目】如图（1），在圆锥内放两个大小不同且不相切的球,使得它们分别与圆锥的侧面、底面相切，用与两球都相切的平面截圆锥的侧面得到截口曲线是椭圆.理由如下：如图（2），若两个球分别与截面相切于点
，在得到的截口曲线上任取一点
，过点作圆锥母线，分别与两球相切于点
，由球与圆的几何性质，得
，
，所以
，且
，由椭圆定义知截口曲线是椭圆，切点为焦点.这个结论在圆柱中也适用，如图（3），在一个高为
，底面半径为
的圆柱体内放球，球与圆柱底面及侧面均相切.若一个平面与两个球均相切，则此平面截圆柱所得的截口曲线也为一个椭圆，则该椭圆的离心率为______.
【答案】
【解析】
根据题意可得椭圆的长轴长和短轴长，再代入离心率方程，即可得答案；
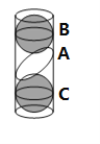
如图所示，
根据题意可得椭圆上的点
到两个切点的距离等于
，
，
，
，
故答案为：.
练习册系列答案
小学生10分钟口算测试100分系列答案
相关题目
