Question

【题目】设数列：A：a1，a2，…，an，B：b1，b2，…，bn.已知ai，bj∈{0，1}（i=1，2，…，n；j=1，2，…，n），定义n×n数表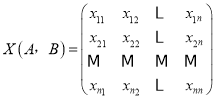，其中xij.

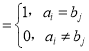（1）若A：1，1，1，0，B：0，1，0，0，写出X（A，B）；

（2）若A，B是不同的数列，求证：n×n数表X（A，B）满足“xij=xji（i=1，2，…，n；j=1，2，…，n；ij）”的充分必要条件为“ak+bk=1（k=1，2，…，n）”；

（3）若数列A与B中的1共有n个，求证：n×n数表X（A，B）中1的个数不大于.

Answer 1

【答案】（1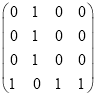）；（2）证明见解析；（3）证明见解析.

【解析】

（1）根据题中给的定义写出X（A，B）；

（2）可先证充分性，充分性由定义易证；再证必要性，注意分类讨论:先分a1=0和a1=1两类，a1=0较易证明，对a1=1再分b1=0和b1=1两类证明，运用xij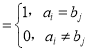分析推理可得;

（3）根据数列A与B中的1共有n个，设A中1的个数为p，则A中0的个数为n﹣p，B中1的个数为n﹣p，B中0的个数为p.表示出n×n数表X（A，B）中1的个数，再用不等式证得n×n数表X（A，B）中1的个数不大于.

（1）解：.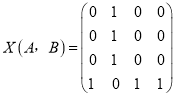

（2）证明：充分性

若ak+bk=1（k=1，2，…，n），由于xij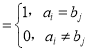，xji，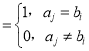

令 A：a1，a2，…，an，由此数列 B：1﹣a1，1﹣a2，…，1﹣an.

由于 ai=bjai=1﹣ajai+aj=1aj=1﹣aiaj=bi.

从而有 xij=xji（i=1，2，…，n；j=1，2，…，n；ij）.

必要性

若xij=xji（i=1，2，…，n；j=1，2，…，n；ij）.

由于A，B是不同的数列，

设a1=1，b1=0，对任意的正整数k＞1，

①若x1k=xk1=1，可得 a1=bk=1，ak=b1=0，

所以 ak+bk=1.

②若x1k=xk1=0，可得 bk=0，ak=1，

所以ak+bk=1.

同理可证 ，b1=1时，有ak+bk=1（k=1，2，…，n）成立.

设a1=1，b1=1，对任意的正整数k＞1，

①若x1k=xk1=1，可得a1=bk=1，ak=b1=1，

所以有ak=bk=1，则A，B是相同的数列，不符合要求.

②若x1k=xk1=0，可得bk=0，ak=0，

所以有ak=bk，则A，B是相同的数列，不符合要求.

同理可证 a1=0，b1=0时，A，B是相同的数列，不符合要求.

综上，有n×n数表X（A，B）满足“xij=xji”的充分必要条件为“ak+bk=1（k=1，2，…，n）”.

（3）证明：由于数列A，B中的1共有n个，设A中1的个数为p，

由此，A中0的个数为n﹣p，B中1的个数为n﹣p，B中0的个数为p.

若 ai=1，则数表X（A，B）的第i行为数列B：b1，b2，…，bn，

若 ai=0，则数表X（A，B）的第i行为数列B：1﹣b1，1﹣b2，…，1﹣bn，

所以 数表X（A，B）中1的个数为.

所以 n×n数表X（A，B）中1的个数不大于.