题目内容
【题目】某公司为了对一种新产品进行合理定价，将该产品按亊先拟定的价格进行试销，得到如下数据：
单价x（元） | 4 | 5 | 6 | 7 | 8 | 9 |
销量V（件） | 90 | 84 | 83 | 80 | 75 | 68 |
由表中数据．求得线性回归方程为 
=﹣4x+a．若在这些样本点中任取一点，則它在回归直线右上方的概率为
（ ）
A.
B.
C.
D.
【答案】C
【解析】解： 
= 
（4+5+6+7+8+9）= 
， 
= （90+84+83+80+75+68）=80 ∵ 
=﹣4x+a，
∴a=106，
∴回归直线方程 =﹣4x+106；
数据（4，90），（5，84），（6，83），（7，80），（8，75），（9，68）．
6个点中有3个点在直线右上方，即（6，83），（7，80），（8，75）．
其这些样本点中任取1点，共有6种不同的取法，
故这点恰好在回归直线右上方的概率P= 
= 
．
故选：C．
练习册系列答案
长江作业本同步练习册系列答案
小天才课时作业系列答案
相关题目
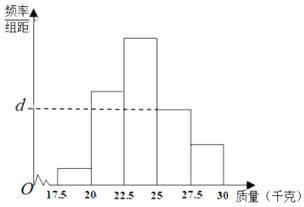
【题目】为了检测某种产品的质量（单位：千克），抽取了一个容量为N的样本，整理得到的数据作出了频率分布表和频率分布直方图如图：
分组 | 频数 | 频率 |
[17.5，20） | 10 | 0.05 |
[20，225） | 50 | 0.25 |
[22.5，25） | a | b |
[25，27.5） | 40 | c |
[27.5，30] | 20 | 0.10 |
合计 | N | 1 |
（Ⅰ）求出表中N及a，b，c的值；
（Ⅱ）求频率分布直方图中d的值；
（Ⅲ）从该产品中随机抽取一件，试估计这件产品的质量少于25千克的概率．
