题目内容
6.甲袋有1个黑球,2个白球,乙袋中有3个白球,每次从两袋中各取一个,交换放入另一袋中,求交换n次后,黑球仍在甲袋中的概率$\frac{1}{6}×(\frac{1}{3})^{n-1}$+$\frac{1}{2}$.分析 设An表示事件交换n次后黑球仍在甲袋中,先利用全概率公式推导出P(An)=$\frac{1}{3}[1+P({A}_{n-1})]$,从而得到P(An)-$\frac{1}{2}$=$\frac{1}{3}$[P(An-1)-$\frac{1}{2}$],由此利用等比数列的性质能求出交换n次后,黑球仍在甲袋中的概率.
解答 解:设An表示事件交换n次后黑球仍在甲袋中,
P(An)=P(An-1)P(An|An-1)+P($\overline{{A}_{n-1}}$)P(An|$\overline{{A}_{n-1}}$)
=$\frac{2}{3}P({A}_{n-1})+\frac{1}{3}[1-P({A}_{n-1})]$
=$\frac{1}{3}P({A}_{n-1})+\frac{1}{3}$,
∴P(An)=$\frac{1}{3}[1+P({A}_{n-1})]$,
∴P(An)-$\frac{1}{2}$=$\frac{1}{3}$[P(An-1)-$\frac{1}{2}$],
由题意得P(A1)=$\frac{2}{3}$,∴P(A1)-$\frac{1}{2}$=$\frac{1}{6}$,
∴由等比数列性质,得P(An)-$\frac{1}{2}$=$\frac{1}{6}×(\frac{1}{3})^{n-1}$,
∴P(An)=$\frac{1}{6}×(\frac{1}{3})^{n-1}$+$\frac{1}{2}$.
故答案为:$\frac{1}{6}×(\frac{1}{3})^{n-1}$+$\frac{1}{2}$.
点评 本题考查概率的求法,是中档题,解题时要注意全概率公式和等比数列的性质的合理运用.

练习册系列答案
相关题目
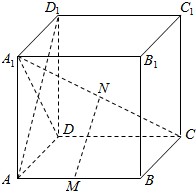 如图所示,在正方体ABCD-A1B1C1D1中,M是AB上一点,N是A1C的中点,MN⊥平面A1DC,求证:
如图所示,在正方体ABCD-A1B1C1D1中,M是AB上一点,N是A1C的中点,MN⊥平面A1DC,求证: