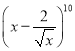题目内容
【题目】椭圆![]() 离心率为
离心率为![]() ,
,![]() ,
,![]() 是椭圆的左、右焦点,以
是椭圆的左、右焦点,以![]() 为圆心,
为圆心,![]() 为半径的圆和以
为半径的圆和以![]() 为圆心、
为圆心、![]() 为半径的圆的交点在椭圆
为半径的圆的交点在椭圆![]() 上.
上.
(1)求椭圆![]() 的方程;
的方程;
(2)设椭圆![]() 的下顶点为
的下顶点为![]() ,直线
,直线![]() 与椭圆
与椭圆![]() 交于两个不同的点
交于两个不同的点![]() ,是否存在实数
,是否存在实数![]() 使得以
使得以![]() 为邻边的平行四边形为菱形?若存在,求出
为邻边的平行四边形为菱形?若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
【答案】(1)![]() ;(2)答案见解析.
;(2)答案见解析.
【解析】试题分析:(1)第一问,直接根据已知条件得到关于a,c的方程组解答即可. (2)第二问,先设MN的中点为H,再利用韦达定理得到点H的坐标,再根据![]() 求出k的值,最后利用判别式检验.
求出k的值,最后利用判别式检验.
试题解析:
(1)由题意可得 ,
,
解得![]() ,
,
所以![]() ,
,
所以椭圆的方程为![]() ;
;
(2)由题意知![]() ,
,
联立方程 ,整理得
,整理得![]() ,
,
![]() (化简可得
(化简可得![]() ),①
),①
设![]() ,则
,则
![]() ,
,![]() ,
,
设![]() 中点为
中点为![]() ,
,
由![]() ,知
,知![]() ,
,
所以点![]() 的坐标为
的坐标为![]() ,
,
因为![]() ,所以
,所以![]() ,
,
又直线![]() 斜率均存在,所以
斜率均存在,所以![]() .
.
于是![]()
 ,
,
解得![]() ,即
,即![]() ,
,
将![]() 代入①,满足
代入①,满足![]() .故存在
.故存在![]() 使得以
使得以![]() 为邻边的平行四边形可以是菱形,
为邻边的平行四边形可以是菱形,![]() 值为
值为![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目