Question

已知集合M={x|y=

3-x2

}，N={y|1≤y≤3}，且M，N都是全集R的子集，则如图韦恩图中阴影部分表示的集合为（　　）

• A．{x|-

  3

  ≤x≤

  3

  }
• B．{y|-1≤y≤3}
• C．{x|

  3

  ＜x≤3}
• D．Φ

Answer 1

分析：由韦恩图中阴影部分表示的集合为N∩（?_RM），然后利用集合的基本运算进行求解即可．

解答：解：M={x|3-x²≥0}={x|x²≤3}={x|-

3

≤x≤

3

}，
∴（?_RM）={x|x＞

3

或x＜-

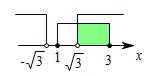
3

}．
由韦恩图中阴影部分表示的集合为N∩（?_RM），
∴N∩（?_RM）={x|x＞

3

或x＜-

3

}∩{y|1≤y≤3}={x|

3

＜x≤3}，
故选C．

点评：本题主要考查集合的基本运算，利用韦恩图确定集合关系，然后利用数轴求基本运算是解决此类问题的基本方法．