题目内容
【题目】已知α为锐角,且 ![]() ,函数
,函数 ![]() ,数列{an}的首项a1=1,an+1=f(an).
,数列{an}的首项a1=1,an+1=f(an).
(1)求函数f(x)的表达式;
(2)求证:数列{an+1}为等比数列;
(3)求数列{an}的前n项和Sn .
【答案】
(1)解:∵ 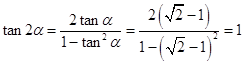
又∵α为锐角
∴α= ![]()
∴ ![]()
∴f(x)=2x+1
(2)证明:∵an+1=2an+1,∴an+1+1=2(an+1)
∵a1=1
∴数列{an+1}是以2为首项,2为公比的等比数列
(3)解:由上步可得an+1=2n,∴an=2n﹣1
∴ ![]()
【解析】(1)由 ![]() ,将
,将 ![]() 代入可求解,由α为锐角,得α=
代入可求解,由α为锐角,得α= ![]() ,从而计算得
,从而计算得 ![]() 进而求得函数表达式.(2)由an+1=2an+1,变形得an+1+1=2(an+1),由等比数列的定义可知数列{an+1}是以2为首项,2为公比的等比数列.(3)由(2)得an=2n﹣1,转化为一个等比数列与一个等差数列的和的形式,可计算得
进而求得函数表达式.(2)由an+1=2an+1,变形得an+1+1=2(an+1),由等比数列的定义可知数列{an+1}是以2为首项,2为公比的等比数列.(3)由(2)得an=2n﹣1,转化为一个等比数列与一个等差数列的和的形式,可计算得 ![]() .
.

 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案【题目】据IEC(国际电工委员会)调查显示,小型风力发电项目投资较少,且开发前景广阔,但受风力自然资源影响,项目投资存在一定风险.根据测算,风能风区分类标准如下:
风能分类 | 一类风区 | 二类风区 |
平均风速m/s | 8.5~10 | 6.5~8.5 |
假设投资A项目的资金为x(x≥0)万元,投资B项目资金为y(y≥0)万元,调研结果是:未来一年内,位于一类风区的A项目获利30%的可能性为0.6,亏损20%的可能性为0.4;位于二类风区的B项目获利35%的可能性为0.6,亏损10%的可能性是0.1,不赔不赚的可能性是0.3.
(1)记投资A,B项目的利润分别为ξ和η,试写出随机变量ξ与η的分布列和期望Eξ,Eη;
(2)某公司计划用不超过100万元的资金投资于A,B项目,且公司要求对A项目的投资不得低于B项目,根据(1)的条件和市场调研,试估计一年后两个项目的平均利润之和z=Eξ+Eη的最大值.