题目内容
1.已知数列{an}满足a1=2,an+1=$\frac{{a}_{n}-1}{{a}_{n}}$,Sn是其前n项和,则S2015=( )| A. | $\frac{2011}{2}$ | B. | 1009 | C. | 1007 | D. | $\frac{2017}{2}$ |
分析 由已知结合数列递推式求出数列前几项,可得数列是以3为周期的周期数列,由此可得S2015.
解答 解:由a1=2,an+1=$\frac{{a}_{n}-1}{{a}_{n}}$,得
${a}_{2}=\frac{{a}_{1}-1}{{a}_{1}}=\frac{1}{2}$,
${a}_{3}=\frac{{a}_{2}-1}{{a}_{2}}=\frac{\frac{1}{2}-1}{\frac{1}{2}}=-1$,
${a}_{4}=\frac{{a}_{3}-1}{{a}_{3}}=\frac{-1-1}{-1}=2$,
由上可知,数列{an}是以3为周期的周期数列,
则S2015=a1+a2+a3+…+a2015=671(a1+a2+a3)+a1+a2
=$671×(2+\frac{1}{2}-1)+$$\frac{5}{2}$=1009.
故选:B.
点评 本题考查数列递推式,关键是对数列周期的发现,是基础题.

练习册系列答案
相关题目
6.已知正项数列{an}满足a1=1,(n+2)an+12-(n+1)a${\;}_{n}^{2}$+anan+1=0,则它的通项公式为( )
| A. | an=$\frac{1}{n+1}$ | B. | an=$\frac{2}{n+1}$ | C. | an=$\frac{n+1}{2}$ | D. | an=n |
11.自点A(1,3)作圆(x+3)2+(y-2)2=1的切线,则切线长为( )
| A. | 4 | B. | $\sqrt{17}$ | C. | $\sqrt{10}$ | D. | 5 |
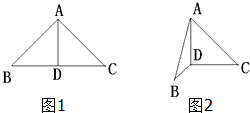 已知Rt△ABC中,AB=AC=a,AD是斜边BC上的高,以AD为折痕使∠BDC成直角,
已知Rt△ABC中,AB=AC=a,AD是斜边BC上的高,以AD为折痕使∠BDC成直角,