题目内容
10.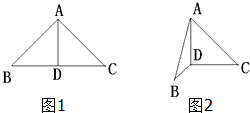 已知Rt△ABC中,AB=AC=a,AD是斜边BC上的高,以AD为折痕使∠BDC成直角,
已知Rt△ABC中,AB=AC=a,AD是斜边BC上的高,以AD为折痕使∠BDC成直角,(1)平面ABD⊥平面BDC,平面ACD⊥平面BDC;
(2)求∠BAC的度数.
分析 (1)由原直角三角形中,AD是斜边BD上的高,得到AD与DB、DC都垂直,利用线面垂直的判定得到AD垂直于面BDC,由线面垂直的性质得到要证得结论;
(2)由原题给出的边的长度,通过解直角三角形分别求出三角形ABC三边的长度,然后利用余弦定理求解∠BAC的大小
解答 (1)证明:∵AD⊥BC,AD⊥DC,BD∩DC=D,∴AD⊥平面BDC.
又AD?平面ABD,AD?平面ACD,∴平面ABD⊥平面BDC,平面ACD⊥平面BDC;
(2)证明:在原Rt△ABC中,AB=AC=a,∴BC=$\sqrt{2}$a,
∴BD=DC=$\frac{\sqrt{2}}{2}$a,
又折叠后∠BDC=90°,
∴△BDC为等腰Rt△,∴BC=a,∴AB=BC=AC,∴∠BAC=60°.
点评 本题考查了平面与平面垂直的判定,考查了点线面间距离的计算,考查了学生的空间想象能力和思维能力,解答的关键是对折叠问题折叠前后的变量与不变量的掌握,是中档题.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案
相关题目
1.已知数列{an}满足a1=2,an+1=$\frac{{a}_{n}-1}{{a}_{n}}$,Sn是其前n项和,则S2015=( )
| A. | $\frac{2011}{2}$ | B. | 1009 | C. | 1007 | D. | $\frac{2017}{2}$ |
2.集合N={x|x2-3x+2=0}等于( )
| A. | {(1,2)} | B. | {1,2} | C. | ∅ | D. | 1,2 |
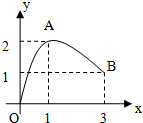 如图,函数f(x)的图象是曲线段OAB,其中点O,A,B的坐标分别为(0,0),(1,2),(3,1),则f[$\frac{1}{f(3)}$]的值为2.
如图,函数f(x)的图象是曲线段OAB,其中点O,A,B的坐标分别为(0,0),(1,2),(3,1),则f[$\frac{1}{f(3)}$]的值为2.