题目内容
6.已知正项数列{an}满足a1=1,(n+2)an+12-(n+1)a${\;}_{n}^{2}$+anan+1=0,则它的通项公式为( )| A. | an=$\frac{1}{n+1}$ | B. | an=$\frac{2}{n+1}$ | C. | an=$\frac{n+1}{2}$ | D. | an=n |
分析 由数列递推式可得$(n+2)•(\frac{{a}_{n+1}}{{a}_{n}})^{2}+\frac{{a}_{n+1}}{{a}_{n}}=n+1$,即$\frac{{a}_{n+1}}{{a}_{n}}=\frac{n+1}{n+2}$.然后利用累积法求出数列的通项公式.
解答 解:由(n+2)an+12-(n+1)a${\;}_{n}^{2}$+anan+1=0,得
$(n+2)•(\frac{{a}_{n+1}}{{a}_{n}})^{2}+\frac{{a}_{n+1}}{{a}_{n}}=n+1$,即$\frac{{a}_{n+1}}{{a}_{n}}=\frac{n+1}{n+2}$.
∴${a}_{n}=\frac{{a}_{n}}{{a}_{n-1}}•\frac{{a}_{n-1}}{{a}_{n-2}}…\frac{{a}_{2}}{{a}_{1}}•{a}_{1}$=$\frac{n}{n+1}•\frac{n-1}{n}…\frac{2}{3}•1$=$\frac{2}{n+1}$.
故选:B.
点评 本题考查数列递推式,考查了累积法求数列的通项公式,是中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.已知等差数列{an}的通项公式an=$\frac{64-4n}{5}$,设An=|an+an+1+…+an+12|(n∈N*),当An取得最小值时,n的取值是( )
| A. | 16 | B. | 14 | C. | 12 | D. | 10 |
1.已知数列{an}满足a1=2,an+1=$\frac{{a}_{n}-1}{{a}_{n}}$,Sn是其前n项和,则S2015=( )
| A. | $\frac{2011}{2}$ | B. | 1009 | C. | 1007 | D. | $\frac{2017}{2}$ |
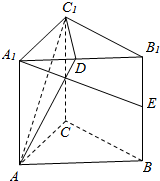 如图,在直三棱柱ABC-A1B1C1中,AC=BC,侧面BB1A1是正方形,D,E分别为A1B1和BB1的中点.求证:A1E⊥平面AC1D.
如图,在直三棱柱ABC-A1B1C1中,AC=BC,侧面BB1A1是正方形,D,E分别为A1B1和BB1的中点.求证:A1E⊥平面AC1D.