题目内容
17. 如图,点B是以AC为直径的圆周上的一点,AB=BC,AC=4,PA=AB,PA⊥平面ABC,点E为PB的中点.
如图,点B是以AC为直径的圆周上的一点,AB=BC,AC=4,PA=AB,PA⊥平面ABC,点E为PB的中点.(Ⅰ)求证:平面AEC⊥平面PBC;
(Ⅱ)求直线AE与平面PAC所成角的大小.
分析 (Ⅰ)证明BC⊥面PAC,推出BC⊥AE,然后证明AE⊥PB,推出AE⊥平面PBC,然后证明平面AEC⊥平面PBC.
(Ⅱ)作BO⊥平面APC,取PO的中点G,连结EG,连结AG,说明∠EAG就是直线AE与平面PAC所成角,通过解三角形求解即可.
解答 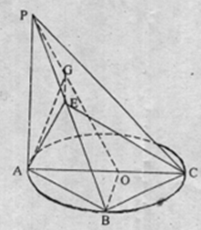 证明:(Ⅰ)∵PA⊥⊙O所在平面,且BC为⊙O的弦,
证明:(Ⅰ)∵PA⊥⊙O所在平面,且BC为⊙O的弦,
∴PA⊥BC
∵AB为⊙O的直径,
∴BC⊥AC.
而PA∩AC=A.
∴BC⊥面PAC,
∵AE?平面PAC,∴BC⊥AE,
∵PA=AB,PA⊥平面ABC,点E为PB的中点.
∴AE⊥PB,PB∩BC=B,
∴AE⊥平面PBC.
∵AE?平面AEC,
∴平面AEC⊥平面PBC.
(Ⅱ)作BO⊥平面APC,取PO的中点G,连结EG,
则EG∥BO,⇒EG⊥平面PAC,连结AG,
∴∠EAG就是直线AE与平面PAC所成角,
AE=$\frac{1}{2}$PB=2,$GE=\frac{1}{2}OB=1$,
∴sin∠EAG=$\frac{GE}{AE}$=$\frac{1}{2}$,
∴直线AE与平面PAC所成角为:$\frac{π}{6}$.
点评 本题考查的知识点是直线与平面垂直的判定,直线与平面所成角的求法,其中熟练掌握空间线面垂直、平行的判定、性质,善于根据直角三角形、圆周角的性质,判断出直线与直线垂直是解答本题的关键.

练习册系列答案
 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
2.若A是正数a、b的等差中项,正数G是a、b的等比中项,则以下结论最准确的是( )
| A. | ab>AG | B. | ab≤AG | C. | ab≥AG | D. | ab<AG |
