题目内容
8.在正方体ABCD-A′B′C′D′中,过对角线BD′的一个平面交AA′于E,交CC′于F①四边形BFD′E一定是平行四边形
②四边形BFD′E有可能是正方形
③四边形BFD′E在底面ABCD内的投影一定是正方形
④四边形BFD′E有可能垂直于平面BB′D′D
以上结论正确的为①③④(写出所有正确结论的编号)
分析 根据面面平行和正方体的几何特征进行判断,利用一些特殊情况进行说明
解答 解:解:如图: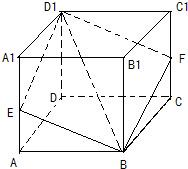
①由平面BCB1C1∥平面ADA1D1,并且B、E、F、D1四点共面,
∴ED1∥BF,同理可证,FD1∥EB,故四边形BFD1E一定是平行四边形,故①正确;
②若BFD1E是正方形,有ED1⊥BE,这个与A1D1⊥BE矛盾,故②错误;
③由图得,BFD1E在底面ABCD内的投影一定是正方形ABCD,故③正确;
④当点E和F分别是对应边的中点时,平面BFD1E⊥平面BB1D1,故④正确.
故答案为:①③④.
点评 本题主要考查了正方体的几何特征,利用面面平行和线线垂直,以及特殊情况进行判断,考查了空间信息能力和逻辑思维能力

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
16.已知函数y=x3+ax2+(a+6)x-1有极大值和极小值,则a的取值范围是( )
| A. | -1<a<2 | B. | -3<a<6 | C. | a<-3或a>6 | D. | a<-1或a>2 |
 如图,在棱长为1的正方体ABCD-A1B1C1D1中,E点在棱DD1上.
如图,在棱长为1的正方体ABCD-A1B1C1D1中,E点在棱DD1上. 每天的P值是空气质量的重要指标,空气质量级别与P值范围对应关系如表所示,为了了解某市2014年的空气质量,随机抽取了该市2014年10天的P值数据,绘制成茎叶图如图所示.
每天的P值是空气质量的重要指标,空气质量级别与P值范围对应关系如表所示,为了了解某市2014年的空气质量,随机抽取了该市2014年10天的P值数据,绘制成茎叶图如图所示. 如图,点B是以AC为直径的圆周上的一点,AB=BC,AC=4,PA=AB,PA⊥平面ABC,点E为PB的中点.
如图,点B是以AC为直径的圆周上的一点,AB=BC,AC=4,PA=AB,PA⊥平面ABC,点E为PB的中点.