题目内容
【题目】如图,已知双曲线 ![]() (a>0,b>0)的左、右焦点分别为F1、F2 , |F1F2|=8,P是双曲线右支上的一点,直线F2P与y轴交于点A,△APF1的内切圆在边PF1上的切点为Q,若|PQ|=2,则该双曲线的离心率为( )
(a>0,b>0)的左、右焦点分别为F1、F2 , |F1F2|=8,P是双曲线右支上的一点,直线F2P与y轴交于点A,△APF1的内切圆在边PF1上的切点为Q,若|PQ|=2,则该双曲线的离心率为( ) 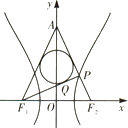
A.![]()
B.![]()
C.2
D.3
【答案】C
【解析】解:如图记AF1、AF2与△APF1的内切圆相切于N、M;
则AN=AM,PM=PQ,NF1=QF1 , AF1=AF2;
则NF1=AF1﹣AN=AF2﹣AM=MF2;
则QF1=MF2;
则PF1﹣PF2=(QF1+PQ)﹣(MF2﹣PM)
=QF1+PQ﹣MF2+PM
=PQ+PM=2PQ=4,
即2a=4,则a=2.
由F1F2=8=2c,得c=4,
则e= ![]() =2.
=2.
故选:C.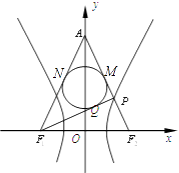

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目