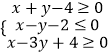Question

【题目】若f（x）是定义在（0，+∞）上的函数，当x＞1时，f（x）＞0，且满足 ．
（1）求f（1）的值；
（2）判断并证明函数的单调性；
（3）若f（2）=1，解不等式 ．

Answer 1

【答案】
（1）解：令x=y=1可得f（1）=f（1）﹣f（1）=0
（2）解：设x1＞x2＞0，

则f（x1）﹣f（x2）=f（ ），

∵x1＞x2＞0，∴ ＞1，∴f（ ）＞0，

∴f（x1）﹣f（x2）＞0，即f（x1）＞f（x2），

∴f（x）在（0，+∞）上是增函数

（3）解：∵f（2）=1，∴f（ ）=f（1）﹣f（2）=﹣1，

∴f（4）=f（2）﹣f（ ）=2，

∵ ，

∴f（x2+3x）＜f（4）．

∴ ，

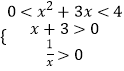解得0＜x＜1．

∴不等式 的解集是（0，1）

【解析】（1）将1看作是本小题的关键，在很多解题中1与0都起到了很重要的作用；（2）根据函数单调性的定义及抽象函数的特点解题；（3）利用前两小题的结论先求出函数值为2的自变量，再利用其单调性列出第一个不等式，第二与第三个不等式是根据函数的定义域列出的.