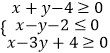题目内容
【题目】已知函数 ![]() ,其中a为常数.
,其中a为常数.
(1)若a=1,判断函数f(x)的奇偶性;
(2)若函数 ![]() 在其定义域上是奇函数,求实数a的值.
在其定义域上是奇函数,求实数a的值.
【答案】
(1)解:当a=1时, ![]() ,其定义域为R.
,其定义域为R.
此时对任意的x∈R,都有 ![]()
所以函数f(x)在其定义域上为奇函数
(2)解:若函数 ![]() 在其定义域上是奇函数,则对定义域内的任意x,
在其定义域上是奇函数,则对定义域内的任意x,
有: ![]()
整理得:a2e2x﹣1=e2x﹣a2,即:e2x(a2﹣1)=1﹣a2对定义域内的任意x都成立.
所以a2=1
当a=1时, ![]() ,定义域为R;
,定义域为R;
当a=﹣1时, ![]() ,定义域为(﹣∞,0)∪(0,+∞).
,定义域为(﹣∞,0)∪(0,+∞).
所以实数a的值为a=1或a=﹣1.
【解析】(1)根据函数奇偶性的定义进行判断.(2)根据函数是奇函数,建立方程关系进行求解即可.
【考点精析】本题主要考查了函数的奇偶性和函数奇偶性的性质的相关知识点,需要掌握偶函数的图象关于y轴对称;奇函数的图象关于原点对称;在公共定义域内,偶函数的加减乘除仍为偶函数;奇函数的加减仍为奇函数;奇数个奇函数的乘除认为奇函数;偶数个奇函数的乘除为偶函数;一奇一偶的乘积是奇函数;复合函数的奇偶性:一个为偶就为偶,两个为奇才为奇才能正确解答此题.

练习册系列答案
相关题目
【题目】某企业生产甲、乙两种产品均需用A,B两种原料.已知生产1吨每种产品所需原料及每天原料的可用限额如表所示.如果生产一吨甲、乙产品可获得利润分别为3万元、4万元,则该企业每天可获得最大利润为( )
甲 | 乙 | 原料限额 | |
A(吨) | 3 | 2 | 12 |
B(吨) | 1 | 2 | 8 |
A.12万元
B.16万元
C.17万元
D.18万元