题目内容
如图,△ABC与△ACD都是等腰直角三角形,且AD=DC=2,AC=BC,平面DAC⊥平面ABC,如果以ABC平面为水平平面,正视图的观察方向与AB垂直,则三棱锥D-ABC左视图的面积为______.
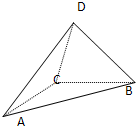

由题意知几何体的左视图是一个三角形,
三角形的一条边长是DC,
过C向AB做垂线,垂足为F,连接D与垂足F,
这个三角形的投影就是左视图,左视图三角形,
由图形及勾股定理可知CF的长度为1,即左视图底边长为1,D到底面的距离是
,故左视图的高是
,
∴三角形的面积是
×1×
=
,
故答案为:
三角形的一条边长是DC,

过C向AB做垂线,垂足为F,连接D与垂足F,
这个三角形的投影就是左视图,左视图三角形,
由图形及勾股定理可知CF的长度为1,即左视图底边长为1,D到底面的距离是
| 2 |
| 2 |
∴三角形的面积是
| 1 |
| 2 |
| 2 |
| ||
| 2 |
故答案为:
| ||
| 2 |

练习册系列答案
相关题目







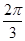 ,那么它的表面积为___________.
,那么它的表面积为___________.