题目内容
【题目】已知函数![]() .
.
(Ⅰ)讨论函数![]() 的单调性;
的单调性;
(Ⅱ)证明:当![]() 时,函数
时,函数![]() 有最大值.设
有最大值.设![]() 的最大值为
的最大值为![]() ,求函数
,求函数![]() 的值域.
的值域.
【答案】(Ⅰ)答案见解析.(Ⅱ)答案见解析.
【解析】
(Ⅰ)![]() ,令
,令![]()
![]() ,然后根据判别式
,然后根据判别式![]() 的符号讨论函数
的符号讨论函数![]() 函数值的情况,进而得到
函数值的情况,进而得到![]() 的符号,于是可得函数的单调情况.
的符号,于是可得函数的单调情况.
(Ⅱ)由题意得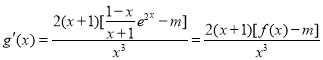 ,结合(Ⅰ)得当
,结合(Ⅰ)得当![]() 时,
时,![]() 在
在![]() 上单调递减,且
上单调递减,且![]() ,因此得到对任意
,因此得到对任意![]() ,存在唯一的
,存在唯一的![]() ,使
,使![]() ,且
,且![]() 在
在![]() 单调递增,在
单调递增,在![]() 单调递减,所以
单调递减,所以![]() 的最大值
的最大值![]() .设
.设![]()
![]() ,则
,则![]() 在
在![]() 单调递减,可得
单调递减,可得![]() ,进而可得所求值域.
,进而可得所求值域.
(Ⅰ)由![]() ,
,
得![]() .
.
令![]() ,
,
则![]() ,
,
(1)当![]() 时,
时,![]() ,所以
,所以![]() ,
,![]() ,
,
所以![]() 在
在![]() 上单调递减.
上单调递减.
(2)当![]() 或
或![]() 时,
时,![]() ,
,
设![]() 的两根为
的两根为![]() 且
且![]() ,则
,则![]() ,
,
①若![]() ,可知
,可知![]() ,
,
则当![]() 时,
时,![]() 单调递减;当
单调递减;当![]() 时,
时,![]() 单调递增.
单调递增.
②若![]() ,可知
,可知![]() ,
,
则当![]() 时,
时,![]() 单调递减;
单调递减;
当![]() 时,
时,![]() 单调递增.
单调递增.
综上可知:
当![]() 时,
时,![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增;
上单调递增;
当![]() 时,
时,![]() 在
在![]() 上单调递减;
上单调递减;
当![]() 时,
时,![]() 在
在![]() ,
,![]() 上单调递减,在
上单调递减,在![]() 上单调递增.
上单调递增.
(Ⅱ)由![]() ,
,
得![]()
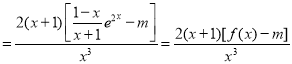 ,
,
由(Ⅰ)可知当![]() 时,
时,![]() 在
在![]() 上单调递减,且
上单调递减,且![]() ,
,
所以对任意![]() ,存在唯一的
,存在唯一的![]() ,使
,使![]() (反之对任意
(反之对任意![]() ,
,
也存在唯一![]() ,使
,使![]() ).
).
且当![]() 时,
时,![]() ,
,![]() ,
,![]() 在
在![]() 单调递增;
单调递增;
当![]() 时,
时,![]() ,
,![]() ,
,![]() 在
在![]() 单调递减.
单调递减.
因此当![]() 时,
时,![]() 取得最大值,且最大值
取得最大值,且最大值![]()
![]()
![]() ,
,
令![]() ,
,
则![]() ,
,
所以![]() 在
在![]() 单调递减,
单调递减,
所以![]() ,即
,即![]() ,
,
所以![]() 的值域为
的值域为![]() .
.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目