题目内容
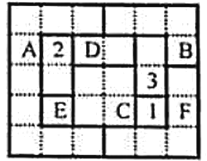
【题目】四色猜想是世界三大数学猜想之一,1976年美国数学家阿佩尔与哈肯证明了四色定理.其内容是:“任意一张平面地图只用四种颜色就能使具有共同边界的国家涂上不同的颜色.”用数学语言表示为“将平面任意地细分为不相重叠的区域,每一个区域总可以用1,2,3,4四个数字之一标记,而不会使相邻的两个区域得到相同的数字.”如图,网格纸上小正方形的边长为1,粗实线围成的各区域(如区域D由两个边长为1的小正方形构成)上分别标有数字1,2,3,4的四色地图符合四色定理,区域A、B、C、D、E、F标记的数字丢失若在该四色地图上随机取一点,则恰好取在标记为4的区域的概率是
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】B
【解析】
根据相邻的两个区域必须是不同的数字这一规则,逐个区域进行判断,区域C相邻给定的标记为1,2,3的区域,从而可以最先判断,最后可根据几何概型的概率求法来求得概率.
因为区域C相邻标记1,2,3的区域,所以区域C标记4,进而区域D相邻标记2,3,4的区域,从而推出区域D标记1,区域A相邻标记1,2,4的区域,所以区域A标记3,区域E相邻标记2,3,4的区域,从而区域E标记1,区域F相邻标记1,3,4的区域,从而标记2,区域B相邻标记为1,2,3的区域,所以标记4,所以只有B,C标记为4,共占8个边长为1的正方形,面积为8,总共的区域面积为30,所以在该四色地图上随机取一点,则恰好取在标记为4的区域的概率是![]() ,故选B.
,故选B.

练习册系列答案
相关题目