题目内容
(15分)已知以点C (t, )(t∈R , t ≠ 0)为圆心的圆与 轴交于点O、A,与y轴交于点O、B,其中O为原点.(1)求证:△OAB的面积为定值;(2)设直线y = –2x+4与圆C交于点M, N,若OM = ON,求t的值并求出圆C的方程.
轴交于点O、A,与y轴交于点O、B,其中O为原点.(1)求证:△OAB的面积为定值;(2)设直线y = –2x+4与圆C交于点M, N,若OM = ON,求t的值并求出圆C的方程.
 轴交于点O、A,与y轴交于点O、B,其中O为原点.(1)求证:△OAB的面积为定值;(2)设直线y = –2x+4与圆C交于点M, N,若OM = ON,求t的值并求出圆C的方程.
轴交于点O、A,与y轴交于点O、B,其中O为原点.(1)求证:△OAB的面积为定值;(2)设直线y = –2x+4与圆C交于点M, N,若OM = ON,求t的值并求出圆C的方程.(1) ,
,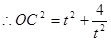 .
.
设圆 的方程是
的方程是 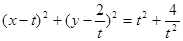
令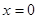 ,得
,得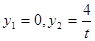 ;令
;令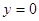 ,得
,得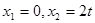
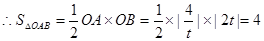 ,即:
,即: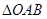 的面积为定值.------6分
的面积为定值.------6分
(2)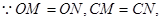
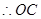 垂直平分线段
垂直平分线段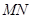 .
.
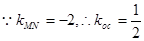 ,
,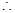 直线
直线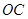 的方程是
的方程是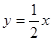 .
.
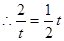 ,解得:
,解得: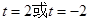 -----------------9分
-----------------9分
当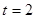 时,圆心
时,圆心 的坐标为
的坐标为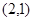 ,
,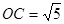 ,
,
此时 到直线
到直线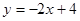 的距离
的距离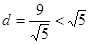 ,
,
圆 与直线
与直线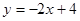 相交于两点。------------------12分. ----
相交于两点。------------------12分. ----
当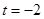 时,圆心
时,圆心 的坐标为
的坐标为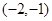 ,
,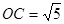 ,
,
此时 到直线
到直线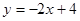 的距离
的距离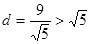
圆 与直线
与直线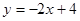 不相交,
不相交,
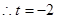 不符合题意舍去. ------------------14分
不符合题意舍去. ------------------14分
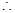 圆
圆 的方程为
的方程为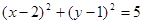 .------------15分
.------------15分
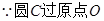 ,
,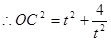 .
.设圆
 的方程是
的方程是 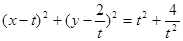
令
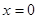 ,得
,得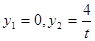 ;令
;令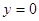 ,得
,得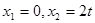
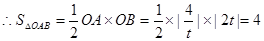 ,即:
,即: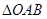 的面积为定值.------6分
的面积为定值.------6分(2)
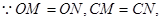
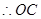 垂直平分线段
垂直平分线段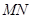 .
.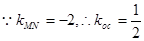 ,
, 直线
直线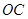 的方程是
的方程是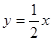 .
.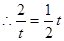 ,解得:
,解得: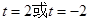 -----------------9分
-----------------9分当
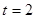 时,圆心
时,圆心 的坐标为
的坐标为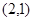 ,
,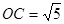 ,
, 此时
 到直线
到直线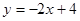 的距离
的距离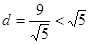 ,
,圆
 与直线
与直线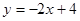 相交于两点。------------------12分. ----
相交于两点。------------------12分. ----当
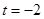 时,圆心
时,圆心 的坐标为
的坐标为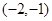 ,
,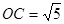 ,
,此时
 到直线
到直线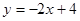 的距离
的距离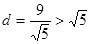
圆
 与直线
与直线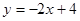 不相交,
不相交,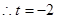 不符合题意舍去. ------------------14分
不符合题意舍去. ------------------14分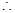 圆
圆 的方程为
的方程为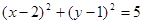 .------------15分
.------------15分(1)求出半径,写出圆的方程,再解出A、B的坐标,表示出面积即可.
(2)通过题意解出OC的方程,解出t 的值,直线y=-2x+4与圆C交于点M,N,判断t是否符合要求,可得圆的方程.
解:(1)∵圆C过原点O,
∴OC2=t2+ ,
,
设圆C的方程是(x-t)2+(y-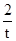 )2=t2+
)2=t2+ ,
,
令x=0,得y1=0,y2=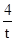 ,
,
令y=0,得x1=0,x2=2t
∴S△OAB=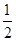 OA×OB=
OA×OB=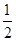 ×|
×|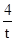 |×|2t|=4,
|×|2t|=4,
即:△OAB的面积为定值;
(2)∵OM=ON,CM=CN,
∴OC垂直平分线段MN,
∵kMN=-2,∴koc=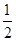 ,
,
∴直线OC的方程是y=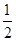 x,
x,
∴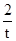 =
=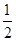 t,解得:t=2或t=-2,
t,解得:t=2或t=-2,
当t=2时,圆心C的坐标为(2,1),OC=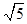
此时C到直线y=-2x+4的距离d=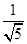 <
<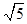 ,
,
圆C与直线y=-2x+4相交于两点,
当t=-2时,圆心C的坐标为(-2,-1),OC=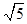 此时C到直线y=-2x+4的距离d=
此时C到直线y=-2x+4的距离d=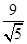 >
>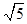 ,
,
圆C与直线y=-2x+4不相交,
∴t=-2不符合题意舍去,
∴圆C的方程为(x-2)2+(y-1)2=5.
(2)通过题意解出OC的方程,解出t 的值,直线y=-2x+4与圆C交于点M,N,判断t是否符合要求,可得圆的方程.
解:(1)∵圆C过原点O,
∴OC2=t2+
 ,
,设圆C的方程是(x-t)2+(y-
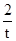 )2=t2+
)2=t2+ ,
,令x=0,得y1=0,y2=
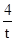 ,
,令y=0,得x1=0,x2=2t
∴S△OAB=
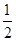 OA×OB=
OA×OB=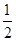 ×|
×|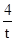 |×|2t|=4,
|×|2t|=4,即:△OAB的面积为定值;
(2)∵OM=ON,CM=CN,
∴OC垂直平分线段MN,
∵kMN=-2,∴koc=
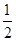 ,
,∴直线OC的方程是y=
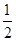 x,
x,∴
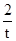 =
=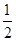 t,解得:t=2或t=-2,
t,解得:t=2或t=-2,当t=2时,圆心C的坐标为(2,1),OC=
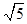
此时C到直线y=-2x+4的距离d=
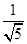 <
<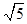 ,
,圆C与直线y=-2x+4相交于两点,
当t=-2时,圆心C的坐标为(-2,-1),OC=
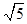 此时C到直线y=-2x+4的距离d=
此时C到直线y=-2x+4的距离d=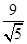 >
>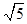 ,
,圆C与直线y=-2x+4不相交,
∴t=-2不符合题意舍去,
∴圆C的方程为(x-2)2+(y-1)2=5.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
 上的点向圆(x-4)2+(y+2)2=1引切线,则切线长的最小值为
上的点向圆(x-4)2+(y+2)2=1引切线,则切线长的最小值为



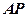 是⊙
是⊙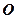 的切线,
的切线,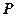 为切点,
为切点,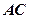 是⊙
是⊙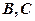 两点,圆心
两点,圆心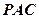 的内部,点
的内部,点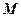 是
是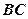 的中点。
的中点。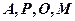 四点共圆;
四点共圆;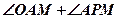 的大小。
的大小。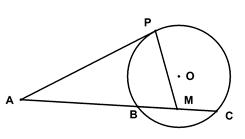
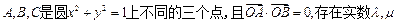 ,且
,且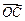 =
=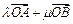
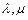 的关系为( )
的关系为( )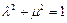
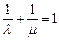
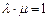
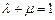
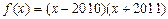 的图象与x轴、y轴有三个交点,有一个圆恰好通过这三个点,则此圆与坐标轴的另一个交点是 ( )
的图象与x轴、y轴有三个交点,有一个圆恰好通过这三个点,则此圆与坐标轴的另一个交点是 ( )


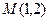 的直线
的直线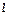 将圆
将圆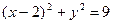 分成两段弧,当其中的优弧最长时,
分成两段弧,当其中的优弧最长时,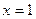
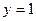
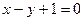

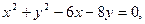 设该圆中过点(3,5)的最
设该圆中过点(3,5)的最 长弦和最短弦分别为AC和BD,则
长弦和最短弦分别为AC和BD,则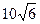
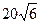
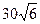
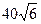
 外一点
外一点 做一条直线与圆
做一条直线与圆 两点,
两点, ,
, 与圆
与圆 点.已知圆
点.已知圆 ,
, ,则
,则 _____.
_____.